Question

【题目】有限个元素组成的集合为，，集合中的元素个数记为，定义，集合的个数记为，当，称集合具有性质.

（1）设集合具有性质，判断集合中的三个元素是否能组成等差数列，请说明理由；

（2） 设正数列的前项和为，满足，其中，数列中的前项：组成的集合记作，将集合中的所有元素从小到大排序，即满足，求；

（3） 己知集合，其中数列是等比数列，，且公比是有理数，判断集合是否具有性质，说明理由.

Answer 1

【答案】（1）否，见解析；（2）；（3）具有性质，理由见解析

【解析】

（1）根据集合具有性质，可以得到、以及的元素性质，运用反证法可以判断出集合中的三个元素不能组成等差数列；

（2）根据递推公式求出数列的通项公式，根据题意写出集合，根据题目中所给的定义，结合等比数列的性质求出；

（3）只要能够证明当时,不成立，运用反证法结合整除的知识，就可以判断出集合具有性质.

（1）集合中的三个元素不能组成等差数列，理由如下：

因为集合具有性质，所以，由题中所给的定义可知：中的元素应是：这6个元素应该互不相等，假设中的三个元素能构成等差数列，不妨设成等差数列，这时有

这与集合元素集合中的6个元素互不相等矛盾，其它二种情况也是一样，故中的三个元素不能能构成等差数列；

（2），得：

，说明数列从第二项起，数列是等差数列，

因为，，所以有，所以，显然也成立，因此.

所以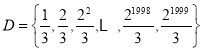

，显然

根据定义在之间增加的元素个数为：，这样包括在内前面一共有个元素.

当时，包括在内前面共有2016个，显然不到第2020个数，所以只有当时，能找到

因此；

（3）集合具有性质，理由如下：设等比数列的公比为，所以通项公式为：，为有理数.

设假设当时,成立，则有

，

因为为有理数，所以设且互质，因此有

，

式子的左边是的倍数，右边是的倍数，而互质，显然不成立，因此集合中的元素个数为：，因此它符合已知所下的定义，因此集合是否具有性质.