
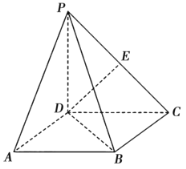
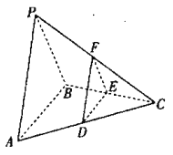
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 中点,
中点,![]() .
.
(1)求证:![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由面面垂直的性质定理可得出![]() 平面
平面![]() ,可得出
,可得出![]() ,由等腰三角形三线合一的性质可得出
,由等腰三角形三线合一的性质可得出![]() ,由此可得出
,由此可得出![]() 平面
平面![]() ,进而得出
,进而得出![]() ;
;
(2)设![]() ,可得出
,可得出![]() ,
,![]() ,由(1)可知,
,由(1)可知,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,可得
,可得![]() ,进而以点
,进而以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,利用空间向量法可求出二面角
轴建立空间直角坐标系,利用空间向量法可求出二面角![]() 的大小.
的大小.
(1)![]() 四边形
四边形![]() 为矩形,则
为矩形,则![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 面
面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() ;
;

(2)不妨设![]() ,由
,由![]() 得
得![]() ,由(1)得
,由(1)得![]() ,∴
,∴![]() ,∴
,∴![]() ,由(1)得
,由(1)得![]() 平面
平面![]() ,
,
由(1)知,![]() 在平面
在平面![]() 的射影为
的射影为![]() ,即
,即![]() ,
,
![]() ,故
,故![]() .
.
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立如下图所示的空间直角坐标系
轴建立如下图所示的空间直角坐标系![]() ,
,
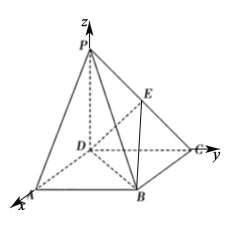
易得![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 与平面
与平面![]() 的法向量分别为
的法向量分别为![]() 和
和![]() ,
,
则![]() ,
,
由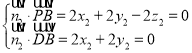 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
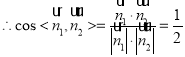 ,设二面角
,设二面角![]() 的大小为
的大小为![]() ,则
,则![]() ,所以二面角
,所以二面角![]() 的大小
的大小![]()


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
(1)确定![]() 的位置(需要说明理由),并证明:平面
的位置(需要说明理由),并证明:平面![]() 平面
平面![]() .
.
(2)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于两点
交于两点![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了减轻家庭困难的高中学生的经济负担,让更多的孩子接受良好的教育,国家施行高中生国家助学金政策,普通高中国家助学金平均资助标准为每生每年1500元,具体标准由各地结合实际在1000元至3000元范围内确定,可以分为两或三档.各学校积极响应政府号召,通过各种形式宣传国家助学金政策.为了解某高中学校对国家助学金政策的宣传情况,拟采用随机抽样的方法抽取部分学生进行采访调查.
(1)若该高中学校有2000名在校学生,编号分别为0001,0002,0003,…,2000,请用系统抽样的方法,设计一个从这2000名学生中抽取50名学生的方案.(写出必要的步骤)
(2)该校根据助学金政策将助学金分为3档,1档每年3000元,2档每年2000元,3档每年1000元,某班级共评定出3个1档,2个2档,1个3档,若从该班获得助学金的学生中选出2名写感想,求这2名同学不在同一档的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )

A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 2017年、2018年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各月仓储指数的中位数与2017年各月仓储指数中位数差异明显
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com