
【题目】已知函数f(x)=2x-![]() .
.
(1)判断函数的奇偶性,并证明;
(2)用单调性的定义证明函数f(x)=2x-![]() 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.
【答案】(1)函数f(x)=2x-![]() 是奇函数.
是奇函数.
证明如下:易知f(x)的定义域为{x|x≠0},关于原点对称.
因为f(-x)=2(-x)-![]() =-2x+
=-2x+![]() =-
=-![]() =-f(x),所以f(x)是奇函数.
=-f(x),所以f(x)是奇函数.
(2)证明:任取x1,x2∈(0,+∞),且x1<x2,
则f(x2)-f(x1)=2x2-![]() -
-![]() =2(x2-x1)+5
=2(x2-x1)+5![]() =(x2-x1)
=(x2-x1)![]() ,
,
因为0<x1<x2,所以x2-x1>0,x1x2>0,
所以f(x2)-f(x1)>0,即f(x2)>f(x1),
所以f(x)=2x-![]() 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.
【解析】
(1)由定义判断![]() 与
与![]() 的关系,即可判断函数奇偶性;
的关系,即可判断函数奇偶性;
(2)由定义证明单调性,假设定义域内的两自变量的值![]() ,作差求
,作差求![]() 的符号,进而判断单调性.
的符号,进而判断单调性.
(1)函数f(x)=2x-![]() 是奇函数.
是奇函数.
证明如下:易知f(x)的定义域为{x|x≠0},关于原点对称.
因为f(-x)=2(-x)-![]() =-2x+
=-2x+![]() =-
=-![]() =-f(x),所以f(x)是奇函数.
=-f(x),所以f(x)是奇函数.
(2)证明:任取x1,x2∈(0,+∞),且x1<x2,
则f(x2)-f(x1)
=2x2-![]() -
-![]()
=2(x2-x1)+5![]()
=(x2-x1)![]() ,
,
因为0<x1<x2,所以x2-x1>0,x1x2>0,
所以f(x2)-f(x1)>0,即f(x2)>f(x1),
所以f(x)=2x-![]() 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.


科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温情况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
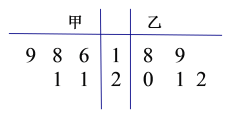
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的平均气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的平均气温的标准差,
其中根据茎叶图能得到的统计结论的编号为( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)若![]() ,过点
,过点![]() ,
, ![]() 的直线
的直线![]() 与抛物线相交于另一点
与抛物线相交于另一点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得
,使得![]() 的长为定值?若存在,求出
的长为定值?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过
不超过![]() 尾/立方米时,
尾/立方米时, ![]() 的值为
的值为![]() 千克/年;当
千克/年;当![]() 时,
时, ![]() 是
是![]() 的一次函数,且当
的一次函数,且当![]() 时,
时, ![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 关于
关于![]() 的函数的表达式.
的函数的表达式.
(![]() )当养殖密度
)当养殖密度![]() 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)=![]() 的定义域为R,其中g(x)为指数函数,且过定点(2,9).
的定义域为R,其中g(x)为指数函数,且过定点(2,9).
(1)求函数f(x)的解析式;
(2)若对任意的t∈[0,5],不等式f(t2+2t+k)+f(-2t2+2t-5)>0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二战中盟军为了知道德国“虎式”重型坦克的数量,采用了两种方法,一种是传统的情报窃取,一种是用统计学的方法进行估计,统计学的方法最后被证实比传统的情报收集更精确,德国人在生产坦克时把坦克从1开始进行了连续编号,在战争期间盟军把缴获的“虎式”坦克的编号进行记录,并计算出这些编号的平均值为675.5,假设缴获的坦克代表了所有坦克的一个随机样本,则利用你所学过的统计知识估计德国共制造“虎式”坦克大约有( )
A.1050辆
B.1350辆
C.1650辆
D.1950辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: ![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com