
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M的轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交曲线C于不同于N的两点A,B,直线NA,NB的斜率分别为k1,k2,求k1+k2的值.
【答案】(1)![]() ;(2)4
;(2)4
【解析】
本题考查椭圆的基本量间的关系及韦达定理的应用
(1)考查椭圆的基本量间的关系
(2)是直线与椭圆相交于![]() 两点,先设出
两点,先设出![]() 两点坐标,本题的突破口是在消参后的方程中找出两根之和、两根之积,整理斜率的表达式,在本问中需考虑直线的斜率是否存在
两点坐标,本题的突破口是在消参后的方程中找出两根之和、两根之积,整理斜率的表达式,在本问中需考虑直线的斜率是否存在
解:(1)由椭圆的定义,可知点M的轨迹是以F1,F2为焦点,![]() 为长轴长的椭圆.
为长轴长的椭圆.
由c=2,a=2![]() ,得b=2.
,得b=2.
故动点M的轨迹C的方程为![]() .
.
(2)当直线l的斜率存在时,设其方程为y+2=k(x+1),
由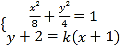 得(1+2k2)x2+4k(k-2)x+2k2-8k=0.
得(1+2k2)x2+4k(k-2)x+2k2-8k=0.
Δ=[4k(k-2)]2-4(1+2k2)(2k2-8k)>0,则k>0或k<-![]()
设A(x1,y1),B(x2,y2),则 ![]() ,
, ![]() .
.
从而![]()
![]()
![]()
当直线l的斜率不存在时,得
所以k1+k2=4.
综上,恒有k1+k2=4.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为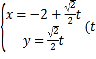 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明设计了一款正四棱锥形状的包装盒,如图所示,![]() 是边长为
是边长为![]() 的正方形硬纸片,切去阴影部分所示的四个全等的等腰三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰三角形,再沿虚线折起,使得![]() 四个点重合于图中的点
四个点重合于图中的点![]() ,正好形成一个正四棱锥形状的包装盒,设正四棱锥底面正方形的边长为
,正好形成一个正四棱锥形状的包装盒,设正四棱锥底面正方形的边长为![]()
![]() .
.

(1)试用![]() 表示该四棱锥的高度
表示该四棱锥的高度![]() ,并指出
,并指出![]() 的取值范围;
的取值范围;
(2)若要求侧面积不小于![]() ,求该四棱锥的高度的最大值,并指出此时该包装盒的容积.
,求该四棱锥的高度的最大值,并指出此时该包装盒的容积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P为两直线l1:3x+4y﹣2=0和l2:2x+y+2=0的交点.
(1)求过P点且与直线3x﹣2y+4=0平行的直线方程;
(2)求过原点且与直线l1和l2围成的三角形为直角三角形的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形仓库用于贮藏食盐已建的仓库的底面直径为![]() ,高
,高![]() ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大![]() (高不变);二是高度增加
(高不变);二是高度增加![]() ,(底面直径不变).
,(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为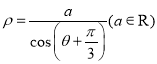 ,直线
,直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() .
.
(1)求实数![]() 的值;
的值;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中有3个红球4个白球,从中取出2个球.下面几个命题:
(1)如果是不放回地抽取,那么取出1个红球,1个白球的概率是![]()
(2)如果是不放回地抽取,那么在至少取出一个红球的条件下,第2次取出红球的概率是![]()
(3)如果是有放回地抽取,那么取出1个红球1个白球的概率是![]()
(4)如果是有放回地抽取,那么第2次取到红球的概率和第1次取到红球的概率相同.
其中正确的命题是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定投掷飞镖3次为一轮,3次中至少两次投中8环以上的为优秀.现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投镖未在8环以上,用1表示该次投镖在8环以上;再以每三个随机数作为一组,代表一轮的结果.例如:“101”代表第一次投镖在8环以上,第二次投镖未在8环以上,第三次投镖在8环以上,该结果代表这一轮投镖为优秀:"100”代表第一次投镖在8环以上,第二次和第三次投镖均未在8环以上,该结果代表这一轮投镖为不优秀.经随机模拟实验产生了如下10组随机数,据此估计,该选手投掷飞镖两轮,至少有一轮可以拿到优秀的概率是( )
101 | 111 | 011 | 101 | 010 | 100 | 100 | 011 | 111 | 001 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com