解:(1)∵f'(x)=3ax
2+(sinθ)x-2
由题设可知

即

由①得:a=
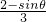
,代入②得:12×
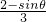
-2sinθ-2≤0,
化简得:sinθ≥1,
∴sinθ=1;
(2)将sinθ=1代入①式得:a=

,则f(x)=

x
3+

x
2-2x+c,
而又由f(1)=

,代入得c=
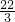
,
∴f(x)=

x
3+

x
2-2x+
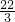
即为所求;
(3)f′(x)=x
2+x-2=(x+2)(x-1)
易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数.
(i)当m>1时,f(x)在[m,m+3]上递增.故f(x)max=f(m+3),f(x)min=f(m)
由f(m+3)-f(m)=

(m+3)
3+

(m+3)
2-2(m+3)-

m
3-

m
2+2m
=3m2+12m+

≤

,得-5≤m≤1.这与条件矛盾故舍去;
(ii)当0≤m≤1时,f(x)在[m,1]上递减,在[1,m+3]上递增,
∴f(x)min=f(1),f(x)max={f(m),f(m+3)}max,
又f(m+3)-f(m)=3m
2+12m+

=3(m+2)
2-

>0(0≤m≤1)
∴f(x)max=f(m+3)
∴|f(x
1)-f(x
2)|≤f(x)max-f(x)min=f(m+3)-f(1)≤f(4)-f(1)=

恒成立,
故当0≤m≤1原式恒成立.
综上:存在m且m∈[0,1]合乎题意.
分析:(1)根据f(x)的解析式求出f(x)的导函数,根据函数f(x)在区间(-2,1)上单调递减,在[1,+∞)上单调递增得到f′(1)=0且f′(-2)≤0,代入导函数分别得到两个关系式记作①和②,由①求出a等于一个关系式,把这个关系式代入②得到sinθ大于等于1,根据正弦函数的值域得到sinθ等于1;
(2)将sinθ的值代入①即可求出a的值,把a的值代入到f(x)中,又因为函数f(x)图象经过点

,即f(1)=

,代入即可求出c的值,即可得到f(x)的解析式;
(3)把a和sinθ的值代入导函数中确定出导函数的解析式,根据导函数的正负得到函数的单调区间,然后分m大于1和m大于等于0小于等于1时,根据函数的单调区间分别求出函数的最小值和最大值,利用最大值和最小值得到|f(x
1)-f(x
2)|的最大值,|f(x
1)-f(x
2)|的最大值小于等于

列出关于m的范围即可求出满足题意的m的范围.
点评:此题考查学生会利用导函数的正负判断函数的单调性,掌握正弦函数的值域及会利用待定系数法求函数的解析式,掌握导数在最值问题中的应用,是一道综合题.

 sinθx2-2x+c的图象经过点
sinθx2-2x+c的图象经过点 ,且在区间(-2,1)上单调递减,在[1,+∞)上单调递增.
,且在区间(-2,1)上单调递减,在[1,+∞)上单调递增. 恒成立,试问:这样的m是否存在,若存在,请求出m的范围;若不存在,说明理由.
恒成立,试问:这样的m是否存在,若存在,请求出m的范围;若不存在,说明理由. 即
即
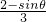 ,代入②得:12×
,代入②得:12×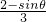 -2sinθ-2≤0,
-2sinθ-2≤0, ,则f(x)=
,则f(x)= x3+
x3+ x2-2x+c,
x2-2x+c, ,代入得c=
,代入得c=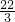 ,
, x3+
x3+ x2-2x+
x2-2x+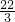 即为所求;
即为所求; (m+3)3+
(m+3)3+ (m+3)2-2(m+3)-
(m+3)2-2(m+3)- m3-
m3- m2+2m
m2+2m ≤
≤ ,得-5≤m≤1.这与条件矛盾故舍去;
,得-5≤m≤1.这与条件矛盾故舍去; =3(m+2)2-
=3(m+2)2- >0(0≤m≤1)
>0(0≤m≤1) 恒成立,
恒成立, ,即f(1)=
,即f(1)= ,代入即可求出c的值,即可得到f(x)的解析式;
,代入即可求出c的值,即可得到f(x)的解析式; 列出关于m的范围即可求出满足题意的m的范围.
列出关于m的范围即可求出满足题意的m的范围.

 名校课堂系列答案
名校课堂系列答案