
分析 可以看出x增大时,f(x)减小,从而判断f(x)为减函数,可利用减函数的定义证明:设任意的x1,x2∈R,且x1<x2,然后作差,通分,结合指数函数的单调性证明f(x1)>f(x2),这便证出函数f(x)在R上为减函数.
解答 解:x增大时,1+2x增大,f(x)减小;
∴f(x)是减函数;
证明:f(x)的定义域为R;
设x1,x2∈R,且x1<x2,则:
$f({x}_{1})-f({x}_{2})=\frac{1}{1+{2}^{{x}_{1}}}-\frac{1}{1+{2}^{{x}_{2}}}$=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$;
∵x1<x2;
∴${2}^{{x}_{2}}>{2}^{{x}_{1}}$;
∴${2}^{{x}_{2}}-{2}^{{x}_{1}}>0$;
∴$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}>0$;
即f(x1)>f(x2);
∴f(x)在R上为减函数.
点评 考查减函数的定义,以及根据减函数的定义证明一个函数为减函数的方法和过程,指数函数的单调性,作差的方法比较f(x1)与f(x2),是分式的一般需通分.


科目:高中数学 来源: 题型:解答题
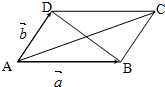 如图在平行四边形ABCD中,M,N分别为DC,BC的中点,已知$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,试用$\overrightarrow a$,$\overrightarrow{b}$表示$\overrightarrow{AC},\overrightarrow{BD},\overrightarrow{AM,}\overrightarrow{AN}$,$\overrightarrow{NM},\overrightarrow{MB}$.
如图在平行四边形ABCD中,M,N分别为DC,BC的中点,已知$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,试用$\overrightarrow a$,$\overrightarrow{b}$表示$\overrightarrow{AC},\overrightarrow{BD},\overrightarrow{AM,}\overrightarrow{AN}$,$\overrightarrow{NM},\overrightarrow{MB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,$\frac{1}{3}$) | B. | (-2,3) | C. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{3}$,+∞) | D. | (-∞,-2)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com