
【题目】已知数列{an}满足:a1= ![]() ,a2=
,a2= ![]() ,2an=an+1+an﹣1(n≥2,n∈N),数列{bn}满足:b1<0,3bn﹣bn﹣1=n(n≥2,n∈R),数列{bn}的前n项和为Sn .
,2an=an+1+an﹣1(n≥2,n∈N),数列{bn}满足:b1<0,3bn﹣bn﹣1=n(n≥2,n∈R),数列{bn}的前n项和为Sn .
(1)求证:数列{bn﹣an}为等比数列;
(2)求证:数列{bn}为递增数列;
(3)若当且仅当n=3时,Sn取得最小值,求b1的取值范围.
【答案】
(1)解:∵2an=an+1+an﹣1(n≥2,n∈N),
∴{an}是等差数列.
又∵a1= ![]() ,a2=
,a2= ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,(n≥2,n∈N*),
,(n≥2,n∈N*),
∴bn+1﹣an+1= ![]()
= ![]() =
= ![]()
= ![]() .
.
又∵ ![]() ,
,
∴{bn﹣an}是以 ![]() 为首项,以
为首项,以 ![]() 为公比的等比数列.
为公比的等比数列.
(2)证明:∵bn﹣an=(b1﹣ ![]() )(
)( ![]() )n﹣1,
)n﹣1, ![]() .
.
∴ ![]() .
.
当n≥2时,bn﹣bn﹣1= ![]() .
.
又b1<0,∴bn﹣bn﹣1>0.
∴{bn}是单调递增数列.
(3)解:∵当且仅当n=3时,Sn取最小值.
∴ ![]() ,即
,即 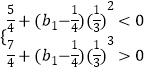 ,
,
∴b1∈(﹣47,﹣11)
【解析】(1)由已知得{an}是等差数列, ![]() ,bn+1﹣an+1=
,bn+1﹣an+1= ![]() =
= ![]() .由此能证明{bn﹣an}是以
.由此能证明{bn﹣an}是以 ![]() 为首项,以
为首项,以 ![]() 为公比的等比数列.(2)由
为公比的等比数列.(2)由 ![]() .得当n≥2时,bn﹣bn﹣1=
.得当n≥2时,bn﹣bn﹣1= ![]() .由此能证明{bn}是单调递增数列.(3)由已知得
.由此能证明{bn}是单调递增数列.(3)由已知得 ![]() ,由此能求出b1的取值范围.
,由此能求出b1的取值范围.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系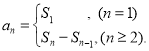 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos(ωx+ ![]() )(其中ω>0,x∈R)的最小正周期为10π.
)(其中ω>0,x∈R)的最小正周期为10π.
(1)求ω的值;
(2)设α,β∈[0, ![]() ],f(5α+
],f(5α+ ![]() )=﹣
)=﹣ ![]() ,f(5β﹣
,f(5β﹣ ![]() )=
)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围.
(2)当x∈[﹣2,2]时,f(x)≥a恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断:
①从个体编号为1,2,…,1000的总体中抽取一个容量为50的样本,若采用系统抽样方法进行抽取,则分段间隔应为20;
②已知某种彩票的中奖概率为 ![]() ,那么买1000张这种彩票就一定会中奖(假设该彩票有足够的张数);
,那么买1000张这种彩票就一定会中奖(假设该彩票有足够的张数);
③从装有2个红球和2个黒球的口袋内任取2个球,恰有1个黒球与恰有2个黒球是互斥但不对立的两个事件;
④设具有线性相关关系的变量的一组数据是(1,3),(2,5),(3,6),(6,8),则它们的回归直线一定过点(3, ![]() ).
).
其中正确的序号是( )
A.①、②、③
B.①、③、④
C.③、④
D.①、③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,椭圆
,椭圆![]() 上任意一点到右焦点
上任意一点到右焦点![]() 距 离的最大值为
距 离的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 满足
满足![]() (
(![]() 为坐标原点),求四边形
为坐标原点),求四边形![]() 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)与直线x+y﹣1=0相交于A、B两点,若a∈[
=1(a>b>0)与直线x+y﹣1=0相交于A、B两点,若a∈[ ![]() ,
, ![]() ],且以AB为直径的圆经过坐标原点O,则椭圆离心率e的取值范围为 .
],且以AB为直径的圆经过坐标原点O,则椭圆离心率e的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com