
如图,在三棱柱![]() 中,
中,
![]() 是正方形
是正方形![]() 的中心,
的中心,![]() ,
,![]() 平面
平面![]() ,且
,且![]()
(Ⅰ)求异面直线AC与A1B1所成角的余弦值;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)设![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 内,且
内,且![]() 平面
平面![]() ,求线段
,求线段![]() 的
的
长.
|
.本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力.满分13分.
方法一:如图所示,建立空间直角坐标系,点B为坐标原点.
依题意得![]()
![]()
 |
(I)解:易得![]() ,
,
于是
所以异面直线AC与A1B1所成角的余弦值为![]()
(II)解:易知![]()
设平面AA1C1的法向量![]() ,
,
则 即
即
不妨令![]() 可得
可得![]() ,
,
同样地,设平面A1B1C1的法向量![]() ,
,
则 即
即 不妨令
不妨令![]() ,
,
可得![]()
于是![]()
从而![]()
所以二面角A—A1C1—B的正弦值为![]()
(III)解:由N为棱B1C1的中点,
得![]() 设M(a,b,0),
设M(a,b,0),
则![]()
由![]() 平面A1B1C1,得
平面A1B1C1,得
即
解得 故
故![]()
因此![]() ,所以线段BM的长为
,所以线段BM的长为![]()
方法二:
(I)解:由于AC//A1C1,故![]() 是异面直线AC与A1B1所成的角.
是异面直线AC与A1B1所成的角.
因为![]() 平面AA1B1B,又H为正方形AA1B1B的中心,
平面AA1B1B,又H为正方形AA1B1B的中心,
![]()
可得![]()
因此![]()
所以异面直线AC与A1B1所成角的余弦值为![]()
 |
(II)解:连接AC1,易知AC1=B1C1,
又由于AA1=B1A1,A1C1=A1=C1,
所以![]() ≌
≌![]() ,过点A作
,过点A作![]() 于点R,
于点R,
连接B1R,于是![]() ,故
,故![]() 为二面角A—A1C1—B1的平面角.
为二面角A—A1C1—B1的平面角.
在![]() 中,
中,![]()
连接AB1,在![]() 中,
中,
![]()
![]() ,
,
从而![]()
所以二面角A—A1C1—B1的正弦值为![]()
(III)解:因为![]() 平面A1B1C1,所以
平面A1B1C1,所以![]()
取HB1中点D,连接ND,由于N是棱B1C1中点,
所以ND//C1H且![]() .
.
又![]() 平面AA1B1B,
平面AA1B1B,
所以![]() 平面AA1B1B,故
平面AA1B1B,故![]()
又![]()
所以![]() 平面MND,连接MD并延长交A1B1于点E,
平面MND,连接MD并延长交A1B1于点E,
则![]()
由![]()
得![]() ,延长EM交AB于点F,
,延长EM交AB于点F,
可得![]() 连接NE.
连接NE.
在![]() 中,
中,
![]()
所以![]()
可得![]()
连接BM,在![]() 中,
中,
![]()


科目:高中数学 来源: 题型:
 如图,在三棱柱中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
如图,在三棱柱中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=| π |
| 3 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年海南省海口市高三高考调研考试理科数学 题型:选择题
如图,在三棱柱 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则 与平面
与平面 所成的角是
所成的角是

A. B.
B. C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高一下学期期末考试数学试卷 题型:解答题
(本小题满分12分)如图,在三棱柱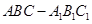 中,
中,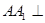 面
面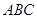 ,
,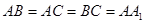 ,
,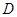 ,
,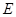 分别为
分别为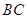 ,
,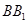 的中点.
的中点.
(1)求证: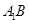 ∥平面
∥平面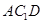 ; (2)求证:
; (2)求证: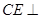 平面
平面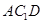 ;
;
(3)直线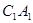 与平面
与平面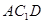 所成的角的正弦值.
所成的角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com