
【题目】已知函数![]() (
(![]() ,且
,且![]() ,e为自然对数的底).
,e为自然对数的底).
(I)求函数![]() 的单调区间
的单调区间
(Ⅱ)若函数![]() 在
在![]() 有两个不同零点,求a的取值范围.
有两个不同零点,求a的取值范围.
【答案】(I)当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;当
;当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I)![]() ,分
,分![]() ,
,![]() 两种情况讨论解不等式即可;
两种情况讨论解不等式即可;
(Ⅱ)因为![]() 有两个正零点,由(I)知
有两个正零点,由(I)知![]() 且
且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.当
上单调递增.当![]() ,当
,当![]() ,
,![]() ,所以只需
,所以只需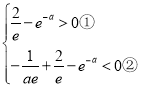 ,对于①直接解不等式,对于②,构造
,对于①直接解不等式,对于②,构造![]() ,结合单调性解决.
,结合单调性解决.
(I)由![]() ,知
,知![]()
①当![]() 时,定义域为
时,定义域为![]() 得
得![]() ,
,![]() 得
得![]() ;
;
②当![]() 时,定义域为
时,定义域为![]() 得
得![]() ,
,![]() 得
得![]()
所以,当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;
;
当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;
;
(Ⅱ)因为![]() 有两个正零点,由(I)知
有两个正零点,由(I)知![]()
且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
设![]() 时,指数函数是爆炸增长,
时,指数函数是爆炸增长,![]() ,
,
当![]() ,当
,当![]() ,
,![]()
因为![]() 有两个正零点,所以有
有两个正零点,所以有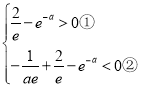 ,
,
由①得![]() ,
,
对于②,令![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,由
,由![]() 知
知![]() ,
,
由②![]() 得
得![]()
综上所述,![]()
【点晴】
本题考查利用导数研究函数的单调性以及已知函数零点个数求参数范围的问题,考查学生逻辑推理能力,是一道中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁、戊5个文艺节目在![]() 三家电视台播放,要求每个文艺节目只能独家播放,每家电视台至少播放其中的一个,则不同的播放方案的种数为( )
三家电视台播放,要求每个文艺节目只能独家播放,每家电视台至少播放其中的一个,则不同的播放方案的种数为( )
A.150B.210C.240D.280
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为支援武汉的防疫,某医院职工踊跃报名,其中报名的医生18人,护士12人,医技6人,根据需要,从中抽取一个容量为n的样本参加救援队,若采用系统抽样和分层抽样,均不用剔除人员.当抽取n+1人时,若采用系统抽样,则需剔除1个报名人员,则抽取的救援人员为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,是奇函数.
,是奇函数.
(1)求实数m的值;
(2)画出函数![]() 的图象,并根据图象求解下列问题;
的图象,并根据图象求解下列问题;
①写出函数![]() 的值域;
的值域;
②若函数![]() 在区间
在区间![]() 上单调递增,求实数a的取值范围.
上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春秋以前中国已有“抱瓮而出灌”的原始提灌方式,使用提水吊杆——桔槔,后发展成辘轳.19世纪末,由于电动机的发明,离心泵得到了广泛应用,为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影,在A处测得B处的仰角为37度,在A处测得C处的仰角为45度,在B处测得C处的仰角为53度,A点所在等高线值为20米,若BC管道长为50米,则B点所在等高线值为( )(参考数据![]() )
)
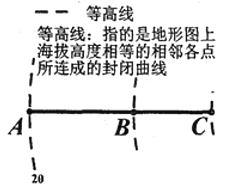
A.30米B.50米C.60米D.70米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】作家马伯庸小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行,每一列上至多有一个紫色小方格(如图所示即满足要求).则一共可以传递______种信息.(用数字作答)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=λn2﹣16n+m.
(1)当λ=2时,求通项公式an;
(2)设{an}的各项为正,当m=15时,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求直线
所成的角为45°,求直线![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在极坐系中,点![]() 绕极点
绕极点![]() 顺时针旋转角
顺时针旋转角![]() 得到点
得到点![]() .以
.以![]() 为原点,极轴为
为原点,极轴为![]() 轴非负半轴,并取相同的单位长度建立平面直角坐标系,曲线
轴非负半轴,并取相同的单位长度建立平面直角坐标系,曲线![]() :
:![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到曲线
得到曲线![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com