
【题目】已知![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求动点![]() 的轨迹方程,并说明轨迹
的轨迹方程,并说明轨迹![]() 是什么图形;
是什么图形;
(2)求动点![]() 与定点
与定点![]() 连线的斜率的最小值;
连线的斜率的最小值;
(3)设直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,是否存在以线段
两点,是否存在以线段![]() 为直径的圆经过
为直径的圆经过![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)动点M的轨迹方程为![]() ,轨迹
,轨迹![]() 是以
是以![]() 为圆心,2为半径的圆;
为圆心,2为半径的圆;
(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)由 ,化简可得:
,化简可得:![]() ,即轨迹
,即轨迹![]() 是以
是以![]() 为圆心,2为半经的圆;(2)设过点
为圆心,2为半经的圆;(2)设过点![]() 的直线为
的直线为![]() ,利用圆心到直线的距离不大于半径即可解得
,利用圆心到直线的距离不大于半径即可解得![]() 的取值范围,从而得出动点
的取值范围,从而得出动点![]() 与定点
与定点![]() 连线的斜率的最小值;(3)假设存在以线段
连线的斜率的最小值;(3)假设存在以线段![]() 为直径的圆经过
为直径的圆经过![]() ,联立方程
,联立方程 ,得
,得![]() ,再利用
,再利用![]() ,求出
,求出![]() 的的值,验证
的的值,验证![]() 是否成立即可.
是否成立即可.
(1) ,化简可得:
,化简可得:![]() ,
,
所以动点M的轨迹方程为![]() .
.
轨迹![]() 是以
是以![]() 为圆心,2为半径的圆.
为圆心,2为半径的圆.
(2)设过点![]() 的直线为
的直线为![]() ,圆心到直线的距离为
,圆心到直线的距离为![]() .
.
∴![]() ,即
,即![]() .
.
(3)假设存在,联立方程得 ,得
,得![]() ,
,
![]() 即
即![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
由题意知![]() ,
,
∴![]() .
.
∴![]() ,得
,得![]() ,
,![]() 且满足
且满足![]() ,
,
∴存在以线段PQ为直径的圆经过A,此时![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是___(请填写所有正确的命题序号).
①命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”;
”;
②命题“若![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
③条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
④已知![]() 时,
时,![]() ,若
,若![]() 是锐角三角形,则
是锐角三角形,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加环保知识竞赛的1200名学生中,随机抽取60名,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后画出如图的频率分布直方图.
后画出如图的频率分布直方图.
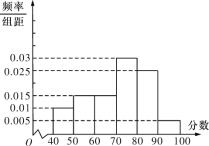
(1)估计这次竞赛成绩的众数与中位数(结果保留小数点后一位);
(2)若这次竞赛成绩不低于80分的同学都可以获得一份礼物,试估计该校参加竞赛的1200名学生中可以获得礼物的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
设![]() 是函数
是函数![]() 的图象上任意两点,且
的图象上任意两点,且![]() ,已知点
,已知点![]() 的横坐标为
的横坐标为![]() .
.
(1)求证:![]() 点的纵坐标为定值;
点的纵坐标为定值;
(2)若![]() 求
求![]() ;
;
(3)已知![]() =
= ,其中
,其中![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,若
项和,若![]() 对一切
对一切![]() 都成立,试求
都成立,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,这三天中恰有两天下雨的概率近似为
A.0.35 B.0.25 C.0.20 D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的食堂中,食堂每天以![]() 元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂某天购进了80斤米粉,以
元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂某天购进了80斤米粉,以![]() (单位:斤)(其中
(单位:斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.
(Ⅰ)计算当天米粉需求量的平均数,并直接写出需求量的众数和中位数;
(Ⅱ) 将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅲ)根据直方图估计该天食堂利润不少于760元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数![]() 与答题正确率
与答题正确率![]() ﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
(2)若用![]() 表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间
表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间![]() 内,则强化训练有效,请问这个班的强化训练是否有效?
内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
![]() =
= ,
, ![]() =
=![]() -
-![]()
![]() ,
,
样本数据![]() 的标准差为:
的标准差为: 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com