
分析 (I)代入三角形的面积公式求出即可;(Ⅱ)通过分类讨论a的范围结合二阶周期点的定义求出a的范围即可.
解答 解:(I)由题,函数f(x)的图象与x轴交于(0,0),(1,0),且有最大值为a,
故所求即为 $\frac{1}{2}$a------(4分)
(Ⅱ)分类讨论如下:
(1)当0<a<$\frac{1}{2}$时,有f(f(x))=$\left\{\begin{array}{l}{{4a}^{2}x,x≤\frac{1}{2}}\\{{4a}^{2}(1-x),x>\frac{1}{2}}\end{array}\right.$,
所以f(f(x))=x只有一个解x=0,又f(0)=0,故0不是二阶周期点.
(2)当a=$\frac{1}{2}$时,有f(f(x))=$\left\{\begin{array}{l}{x,x≤\frac{1}{2}}\\{1-x,x>\frac{1}{2}}\end{array}\right.$,
所以f(f(x))=x有解集{x|x≤$\frac{1}{2}$},
又当x≤$\frac{1}{2}$时,f(x)=x,故{x|x≤$\frac{1}{2}$}中的所有点都不是二阶周期点.
(3)当a>$\frac{1}{2}$时,有f(f(x))=$\left\{\begin{array}{l}{{4x}^{2}x,x≤\frac{1}{4a}}\\{2a-{4a}^{2}x,\frac{1}{4a}<x≤\frac{1}{2}}\\{2a(1-2a)+{4}^{2}x,\frac{1}{2}<x≤\frac{4a-1}{4a}}\\{{4a}^{2}-{4a}^{2}x,x>\frac{4a-1}{4a}}\end{array}\right.$,
所以f(f(x))=x有四个解0,$\frac{2a}{1+{4a}^{2}}$,$\frac{2a}{1+2a}$,$\frac{{4a}^{2}}{1+{4a}^{2}}$,
又f(0)=0,f($\frac{2a}{1+2a}$)=$\frac{2a}{1+2a}$,
f($\frac{2a}{1+{4a}^{2}}$)≠$\frac{2a}{1+{4a}^{2}}$,f($\frac{{4a}^{2}}{1+{4a}^{2}}$)≠$\frac{{4a}^{2}}{1+{4a}^{2}}$,
故只有$\frac{2a}{1+{4a}^{2}}$,$\frac{{4a}^{2}}{1+{4a}^{2}}$是f(x)的二阶周期点,
综上所述,所求a的取值范围为a>$\frac{1}{2}$------(12分)
点评 本题考察了求新定义问题,考察分类讨论思想,是一道中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x2-3x+1 | B. | y=-2x+9 | C. | $y={(\frac{1}{2})^x}$ | D. | y=log2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 仅一个零点且位于区间(c,+∞)内 | |
| B. | 仅一个零点且位于区间(-∞,a)内 | |
| C. | 有两个零点且分别位于区间(a,b)和(b,c)内 | |
| D. | 有两个零点且分别位于区间(-∞,a)和(c,+∞)内 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
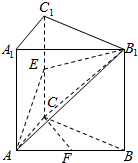 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com