
【题目】下列命题中__________为真命题(把所有真命题的序号都填上).
①“![]() ”成立的必要条件是“
”成立的必要条件是“![]() ”;
”;
②“若![]() 成等差数列,则
成等差数列,则![]() ”的否命题;
”的否命题;
③“已知数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 是等比数列,则
是等比数列,则![]() 成等比数列.”的逆否命题;
成等比数列.”的逆否命题;
④“已知![]() 是
是![]() 上的单调函数,若
上的单调函数,若![]() ,则
,则![]() ”的逆命题.
”的逆命题.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为![]() (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
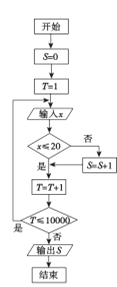
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上.
上.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 向左平移
向左平移![]() 个单位长度后得到
个单位长度后得到![]() ,
,![]() 到
到![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n , 求Tn=a1b1+a2b2+…+anbn的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),并以
为参数),并以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)写出![]() 的极坐标方程,并将
的极坐标方程,并将![]() 化为普通方程;
化为普通方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() 与
与![]() 相交于
相交于![]() 两点,
两点,
求![]() 的面积(
的面积(![]() 为圆
为圆![]() 的圆心).
的圆心).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学校体育节中,某班全体40名同学参加跳绳、踢毽子两项比赛的人数统计如下:
参加跳绳的同学 | 未参加跳绳的同学 | |
参加踢毽的同学 | 9 | 4 |
未参加踢毽的同学 | 7 | 20 |
(1)从该班随机选1名同学,求该同学至少参加上述一项活动的概率;
(2)已知既参加跳绳又参加踢毽的9名同学中,有男生5名,女生4名,现从这5名男生,4名女生中各随机挑选1人,求男同学甲未被选中且女同学乙被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com