
分析 (1)可将原函数变成$f(x)=-1+\frac{2}{{2}^{x}+1}$,根据解析式可以看出,x增大时,f(x)减小,从而判断出该函数为减函数,用减函数的定义证明:设任意的x1,x2∈R,且x1<x2,通过作差的方法证明f(x1)>f(x2)即可得出f(x)在R上单调递减;
(2)根据f(x)为减函数,便得到32a+1>3a-4,从而根据指数函数y=3x的单调性即可得出2a+1>a-4,解该不等式即得实数a的取值范围.
解答 解:(1)$f(x)=\frac{-({2}^{x}+1)+2}{{2}^{x}+1}$=$-1+\frac{2}{{2}^{x}+1}$;
可以看出该函数为减函数,证明如下:
设x1,x2∈R,且x1<x2,则:
$f({x}_{1})-f({x}_{2})=\frac{2}{{2}^{{x}_{1}}+1}-\frac{2}{{2}^{{x}_{2}}+1}$=$\frac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$;
∵x1<x2;
∴${2}^{{x}_{2}}-{2}^{{x}_{1}}>0$,且$({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)>0$;
∴f(x1)>f(x2);
∴f(x)在R上为减函数;
(2)f(x)为减函数;
∴由$f({3}^{2a+1})<f((\frac{1}{3})^{4-a})$得:${3}^{2a+1}>(\frac{1}{3})^{4-a}$;
即32a+1>3a-4;
∴2a+1>a-4;
∴a>-5;
∴实数a的取值范围为(-5,+∞).
点评 考查分离常数法的运用,减函数的定义,以及根据减函数的定义证明函数为减函数的方法和过程,作差法在比较两个实数中的应用,指数函数的单调性.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
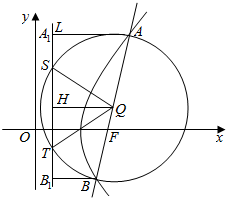 以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证:
以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com