
已知函数f(x)=m(x+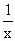 )的图象与函数h(x)=
)的图象与函数h(x)=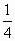 (x+
(x+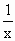 )+2的图象关于点A(0,1)对称.
)+2的图象关于点A(0,1)对称.
(1)求m的值;
(2)若g(x)=f(x)+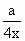 在区间(0,2]上为减函数,求实数a的取值范围.
在区间(0,2]上为减函数,求实数a的取值范围.
|
解:(1)设P(x,y)为函数h(x)图象上一点,点P关于A的对称点为Q( ∵点Q( 将x,y代入得,2-y=m(-x- ∴m= (2)∵g(x)= 则g(x1)-g(x2)= ∴x1x2-(1+a)<0对一切x1,x2∈(0,2]恒成立, ∴由1+a≥x1x2≥4得,a≥3. |


科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知函数f(x)=2acos2x+bsinxcosx,且f(0)=2,f(![]() )=
)=![]() ,
,
(1)求使f(x)>2的x的集合;
(2)若α-β≠kπ(k∈Z),且f(α)=f(β),求tan(α+β)的值.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知函数f(x)=x3+(m-4)x2-3mx+(n-6)(x∈R)的图象关于原点对称,m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明f(x)在区间[-2,2]上是单调函数
(3)当x∈[-2,2]时,不等式f(x)≥(n-logma)logma恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:龙门中学、新丰一中、连平中学三校联考试题、高三数学(理) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2007龙门中学、新丰一中、连平中学三校联考试题、高三数学(文) 题型:044
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com