
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在底面
在底面![]() 的射影为
的射影为![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,依题意有
,依题意有![]() ,
,![]() ,故
,故![]() 平面
平面![]() .根据分析有
.根据分析有![]() ,故
,故![]() 平面
平面![]() ;(2)以
;(2)以![]() 的中点
的中点![]() 为原点,分别以射线
为原点,分别以射线![]() 为
为![]() 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系![]() ,利用向量法求得余弦值为
,利用向量法求得余弦值为![]() .
.
试题解析:
(1)设![]() 为
为![]() 的中点,连接
的中点,连接![]() .由题意得:
.由题意得:![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() ,故
,故![]() 平面
平面![]() .
.
由![]() 分别为
分别为![]() 的中点,得
的中点,得![]() 且
且![]() ,
,
从而![]() 且
且![]() ,所以
,所以![]() 为平行四边形,故
为平行四边形,故![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)方法一:作![]() ,且
,且![]() ,连结
,连结![]() .
.
由![]() ,
,![]() ,得
,得![]() ,
,
由![]() ,
,![]() ,得
,得![]() 与
与![]() 全等.
全等.
由![]() ,得
,得![]() ,因此
,因此![]() 为二面角
为二面角![]() 的平面角.
的平面角.
由![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
由余弦定理得![]() .
.

方法二:
以![]() 的中点
的中点![]() 为原点,分别以射线
为原点,分别以射线![]() 为
为![]() 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系![]() ,如图所示,
,如图所示,
由题意知各点坐标如下:

![]() ,
,![]()
因此![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
由 ,即
,即 ,可取
,可取![]() .
.
由 ,即
,即 ,可取
,可取![]() ,
,
于是![]() .
.
由题意可知,所求二面角的平面角是钝角,故二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sin(
=(sin( ![]() x+φ),1),
x+φ),1), ![]() =(1,cos(
=(1,cos( ![]() x+φ))(ω>0,0<φ<
x+φ))(ω>0,0<φ< ![]() ),记函数f(x)=(
),记函数f(x)=( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() ).若函数y=f(x)的周期为4,且经过点M(1,
).若函数y=f(x)的周期为4,且经过点M(1, ![]() ).
).
(1)求ω的值;
(2)当﹣1≤x≤1时,求函数f(x)的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
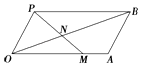
【题目】如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若 ![]() ,
, ![]() .
. 
(1)把y用x表示出来(即求y=f(x)的解析式);
(2)设数列{an}的首项a1=1,前n项和Sn满足Sn=f(Sn﹣1)(n≥2且n∈N*),求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每日生产一种产品![]() 吨,每日生产的产品当日销售完毕,日销售额为
吨,每日生产的产品当日销售完毕,日销售额为![]() 万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了
万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了![]() 的一组统计数据如下表:
的一组统计数据如下表:

(1)请判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() 之间的关系?可从函数增长趋势方面给出简单的理由;
之间的关系?可从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并估计当日产量
的回归方程,并估计当日产量![]() 时,日销售额是多少?(结果保留整数)
时,日销售额是多少?(结果保留整数)
参考公式及数据:线性回归方程![]() 中,
中, ,
,![]() .
.
![]() ,
,![]()
![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各射击一次,击中目标的概率分别是 ![]() 和
和 ![]() .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com