【答案】
分析:设z=x=yi,其中x,y∈R,代入条件化简可得(x
2+y
2-3y)-3xi=1+3i,根据 两个复数相等的充要条件可得
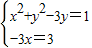
,求出x、y的值,即可得到复数z.
解答:解:设z=x+yi,其中x,y∈R,…(2分)
则
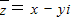
,原方程可以化成:
(x+yi)(x-yi)-3i(x-yi)=1+3i,即 x
2+y
2-3xi-3y=1+3i,
即 (x
2+y
2-3y)-3xi=1+3i.…(6分)
故有
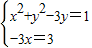
,…(8分)
解得
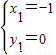
,或
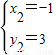
,…(10分)
故z
1=-1,z
2=-1+3i.…(12分)
点评:本题主要考查两个复数代数形式的混合运算,两个复数相等的充要条件,属于基础题.

 .
.