
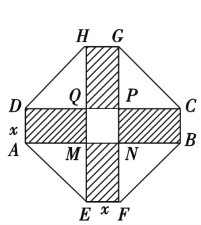
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.

(1)求证:GH∥平面CDE;
(2)求证:面ADEF⊥面ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前三项与数列{bn}的前三项相同,且a1+2a2+22a3+…+2n-1an=8n对任意n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得(bk-ak)∈(0,1)?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
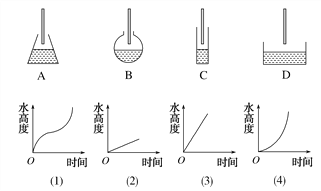
【题目】生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图像,A对应________;B对应________;C对应________;D对应________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
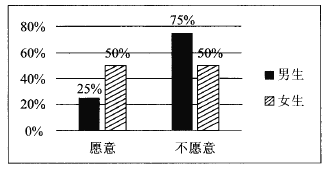
(1)根据条件完成下列![]() 列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者,再从中抽取2人参加挑战,求抽取的2人中至少有一名男生的概率.
参考数据及公式:
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
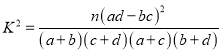 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com