
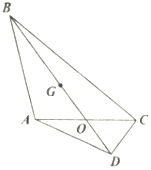
 如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.
如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.分析 (1)由条件利用两个向量的数量积的定义,求得BA•BC的值,可得△ABC的面积S△ABC的值.
(2)以O为原点,AC所在直线为x轴,建立如图所示的平面直角坐标系,设D(x,y),由条件求得点B的坐标,从而求得$\overrightarrow{AD}•\overrightarrow{CD}$的值.
解答  解:(1)∵$\overrightarrow{BA}•\overrightarrow{BC}=32$,∴BA•BCcos30°=32,
解:(1)∵$\overrightarrow{BA}•\overrightarrow{BC}=32$,∴BA•BCcos30°=32,
∴$BA•BC=\frac{32}{{cos{{30}°}}}=\frac{{64\sqrt{3}}}{3}$,
∴${S_{△ABC}}=\frac{1}{2}BA•BCsin{30°}=\frac{1}{2}×\frac{{64\sqrt{3}}}{3}×\frac{1}{2}=\frac{{16\sqrt{3}}}{3}$.
(2)以O为原点,AC所在直线为x轴,建立如图所示的
平面直角坐标系.
则A(-2,0),C(2,0),设D(x,y),
则$\overrightarrow{OD}=({x,y})$,因为$\overrightarrow{OG}$与$\overrightarrow{OD}$互为相反向量,所以$\overrightarrow{OG}=({-x,-y})$.因为G为△ABC的重心,所以$\overrightarrow{OB}=3\overrightarrow{OG}=({-3x,-3y})$,
即B(-3x,-3y),∴$\overrightarrow{BA}=({3x-2,3y}),\overrightarrow{BC}=({3x+2,3y})$,
因此$\overrightarrow{BA}•\overrightarrow{BC}=9{x^2}-4+9{y^2}$=32,即x2+y2=4.
∴$\overrightarrow{AD}•\overrightarrow{CD}=({x+2,y})•({x-2,y})={x^2}+{y^2}-4=0$.
点评 本题主要考查两个向量的数量积的定义,用坐标法求两个向量的数量积,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=ex | B. | y=lnx | C. | y=x2 | D. | y=$\frac{x-1}{x+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [0,2] | C. | [1,2] | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充而分不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 11 | C. | 12 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com