
分析 根据题意,由柯西不等式可得(x+y+z+$\sqrt{yz}$+$\sqrt{zx}$+$\sqrt{xy}$)($\frac{x^2}{{x+\sqrt{yz}}}+\frac{y^2}{{y+\sqrt{zx}}}+\frac{z^2}{{z+\sqrt{xy}}}$)≥(x+y+z)2=9,进而基本不等式分析可得$\sqrt{yz}$+$\sqrt{zx}$+$\sqrt{xy}$≤x+y+z=3,进而可得x+y+z+$\sqrt{yz}$+$\sqrt{zx}$+$\sqrt{xy}$≤6,将其代入(x+y+z+$\sqrt{yz}$+$\sqrt{zx}$+$\sqrt{xy}$)($\frac{x^2}{{x+\sqrt{yz}}}+\frac{y^2}{{y+\sqrt{zx}}}+\frac{z^2}{{z+\sqrt{xy}}}$)≥9中,原不等式即可得到证明.
解答 证明:根据题意,x,y,z为正实数,由柯西不等式可得:
(x+y+z+$\sqrt{yz}$+$\sqrt{zx}$+$\sqrt{xy}$)($\frac{x^2}{{x+\sqrt{yz}}}+\frac{y^2}{{y+\sqrt{zx}}}+\frac{z^2}{{z+\sqrt{xy}}}$)≥(x+y+z)2=9,
即$\frac{x^2}{{x+\sqrt{yz}}}+\frac{y^2}{{y+\sqrt{zx}}}+\frac{z^2}{{z+\sqrt{xy}}}$≥$\frac{9}{x+y+z+\sqrt{yz}+\sqrt{zx}+\sqrt{xy}}$,
而x+y+z=3且x+y≥2$\sqrt{xy}$,x+z≥2$\sqrt{xz}$,z+y≥2$\sqrt{zy}$,
分析可得$\sqrt{yz}$+$\sqrt{zx}$+$\sqrt{xy}$≤x+y+z=3,
又由x+y+z=3,
则x+y+z+$\sqrt{yz}$+$\sqrt{zx}$+$\sqrt{xy}$≤6,
故$\frac{x^2}{{x+\sqrt{yz}}}+\frac{y^2}{{y+\sqrt{zx}}}+\frac{z^2}{{z+\sqrt{xy}}}$≥$\frac{9}{x+y+z+\sqrt{yz}+\sqrt{zx}+\sqrt{xy}}$≥$\frac{9}{6}$=$\frac{3}{2}$;
故可证:$\frac{x^2}{{x+\sqrt{yz}}}+\frac{y^2}{{y+\sqrt{zx}}}+\frac{z^2}{{z+\sqrt{xy}}}$≥$\frac{3}{2}$.
点评 本题主要考查柯西不等式的应用,关键在于对左式的配凑变形,使其满足柯西不等式的条件.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
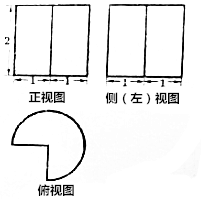
| A. | 3π+4 | B. | 4π+2 | C. | $\frac{9π}{2}$+4 | D. | $\frac{11π}{2}$+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{2}]$ | B. | $(-∞,\frac{1}{2})$ | C. | (-∞,2] | D. | (-∞,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com