
【题目】如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1 , y1)到准线l的距离为d,且d=λp(λ>0). 
(1)若y1=d=1,求抛物线的标准方程;
(2)若 ![]() +λ
+λ ![]() =
= ![]() ,求证:直线AB的斜率为定值.
,求证:直线AB的斜率为定值.
【答案】
(1)解:由条件知,x1=1﹣ ![]() ,则A点坐标为(1﹣
,则A点坐标为(1﹣ ![]() ,1),代入抛物线方程得p=1,
,1),代入抛物线方程得p=1,
∴抛物线方程为y2=2x,
(2)证明:设B(x2,y2),直线AB的方程为y=k(x+ ![]() ),
),
将直线AB的方程代入y2=2px,消去y得: ![]() ,
,
解得:x1= 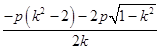 ,x2=
,x2= 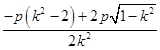 .
.
∵d=λp,
∴ ![]() ,
,
![]() +λ
+λ ![]() =
= ![]() ,
, ![]() ,
,
∴p=x2﹣x1= ![]() ,
,
∴ ![]() ,
,
∴直线AB的斜率为定值.
【解析】(1)由题意可知x1=1﹣ ![]() ,A点坐标为(1﹣
,A点坐标为(1﹣ ![]() ,1),将A点坐标代入抛物线方程求得p的值,写出抛物线的标准方程;(2)直线AB过M(﹣
,1),将A点坐标代入抛物线方程求得p的值,写出抛物线的标准方程;(2)直线AB过M(﹣ ![]() ,0),设直线AB的方程为y=k(x+
,0),设直线AB的方程为y=k(x+ ![]() ),代入抛物线方程y2=2px,消去y,整理得
),代入抛物线方程y2=2px,消去y,整理得 ![]() ,解出x1、x2,将d=x1+
,解出x1、x2,将d=x1+ ![]() ,代入d=λp,得
,代入d=λp,得 ![]() ,
, ![]() +λ
+λ ![]() =
= ![]() ,可知,
,可知, ![]() ,将x1、x2代入,即可解得
,将x1、x2代入,即可解得 ![]() ,可证直线AB的斜率为定值.
,可证直线AB的斜率为定值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点A(1,1),B(3,3),点C在第二象限,且△ABC是以∠BAC为直角的等腰直角三角形.点P(x,y)在△ABC三边围城的区域内(含边界).
(1)若 ![]() +
+ ![]() +
+ ![]() =
= ![]() 求|
求| ![]() |;
|;
(2)设 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),求m+2n的最大值.
(m,n∈R),求m+2n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A.3600
B.1080
C.1440
D.2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系原点O为极点,x轴正方向为极轴,已知曲线C1的参数方程为 ![]() (t为参数),C2的极坐标方程为ρ2(1+sin2θ)=8,C3的极坐标方程为θ=α,α∈[0,π),ρ∈R,
(t为参数),C2的极坐标方程为ρ2(1+sin2θ)=8,C3的极坐标方程为θ=α,α∈[0,π),ρ∈R,
(1)若C1与C3的一个公共点为A(异于O点),且|OA|= ![]() ,求α;
,求α;
(2)若C1与C3的一个公共点为A(异于O点),C2与C3的一个公共点为B,求|OA||OB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax,g(x)= ![]() +a.
+a.
(1)当a=2 时,求F(x)=f(x)﹣g(x)在(0,2]的最大值;
(2)讨论函数F(x)=f(x)﹣g(x) 的单调性;
(3)若f(x)g(x)≤0 在定义域内恒成立,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,动点P在正方体ABCD﹣A1B1C1D1的对角线BD1上.过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,MN=y,则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1(﹣1,0),F2(1,0),曲线C1上任意一点M满足 ![]() ;曲线C2上的点N在y轴的右边且N到F2的距离与它到y轴的距离的差为1.
;曲线C2上的点N在y轴的右边且N到F2的距离与它到y轴的距离的差为1.
(1)求C1 , C2的方程;
(2)过F1的直线l与C1相交于点A,B,直线AF2 , BF2分别与C2相交于点C,D和E,F.求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是关于公差d>0的等差数列{an}的四个命题:p1:数列{an}是递增数列;p2:数列{an}的前n项和Sn是递增数列;p3:数列{ ![]() }是递增数列;p4:数列{an+nd}是递增数列.其中的真命题为( )
}是递增数列;p4:数列{an+nd}是递增数列.其中的真命题为( )
A.p1 , p2
B.p3 , p4
C.p2 , p3
D.p1 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣5|﹣|x﹣2|.
(1)若x∈R,使得f(x)≤m成立,求m的范围;
(2)求不等式x2﹣8x+15+f(x)≤0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com