开学初某校爱心公益社团计划在全校举办一次大型爱心公益活动.计划要从该社团3名男生和3名女生的骨干成员中随机抽取4人组成爱心宣传队．(1)求爱心宣传队中恰有2名女生的概率,(2)求爱心宣传队中至少有2名男生的概率．题目和参考答案——青夏教育精英家教网—

7．开学初某校爱心公益社团计划在全校举办一次大型爱心公益活动，计划要从该社团3名男生和3名女生的骨干成员中随机抽取4人组成爱心宣传队．
（1）求爱心宣传队中恰有2名女生的概率；
（2）求爱心宣传队中至少有2名男生的概率．

分析从该社团3名男生和3名女生的骨干成员中随机抽取4人，共有C₆²=15种，爱心宣传队中恰有2名女生，有C₃²C₃²=9种，爱心宣传队中至少有2名男生，有C₃²C₃²+C₃³C₃¹=12种，根据概率公式计算即可．

解答解：（1）从该社团3名男生和3名女生的骨干成员中随机抽取4人，共有C₆²=15种，
爱心宣传队中恰有2名女生，有C₃²C₃²=9种，
故爱心宣传队中恰有2名女生的概率为$\frac{9}{15}$=$\frac{3}{5}$．
（2）爱心宣传队中至少有2名男生，有C₃²C₃²+C₃³C₃¹=12种，
故爱心宣传队中至少有2名男生的概率为$\frac{12}{15}$=$\frac{4}{5}$．

点评本题考查古典概型及其概率公式，以及排列组合的问题，属基础题．

练习册系列答案

中考英语话题复习浙江工商大学出版社系列答案

中考指要系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

17．设$\overrightarrow{a}$，$\overrightarrow{b}$为平面向量．若$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（3，4），则|$\overrightarrow{a}$|=1，$\overrightarrow{a}$•$\overrightarrow{b}$=3．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

18．设已知{a_n}是递增的等比数列，若a₂=2，a₄-a₃=4，
（Ⅰ）求首项a₁及公比q的值；
（Ⅱ）求数列{a_n}的第5项a₅的值及前5项和S₅的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．

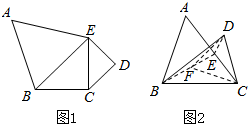如图1，平面五边形ABCDE中，△ABE是边长为2的正三角形，△BCE、△CDE均为等腰直角三角形，且∠BCE和∠CDE为直角，现将△ABE、△CDE分别沿BE、CE折起，使平面ABE⊥平面BCE，平面DCE⊥平面BCE，如图2所示．
（1）求三棱锥C-BDE的体积；
（2）问：在BE上是否存在点F，使得平面DCF⊥平面ABE？若存在，求出点F的位置；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．若曲线y=x²在点（x₀，x₀²）处切线的倾斜角为$\frac{π}{4}$，则x₀=（　　）

A．

B．

C．

$\frac{1}{2}$

D．

$\frac{1}{4}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．（1）计算：（-$\frac{1}{\sqrt{3}-1}$）⁰-$\sqrt{（-5）^{2}}$+8${\;}^{\frac{1}{3}}$+lg2+lg5；
（2）解方程：log₅（2-9•5^x）=-1．