
【题目】如图,在四棱锥A-BCDE中,底面BCDE是等腰梯形,BC∥ DE,∠ DCB=45°,O是BC中点,AO=![]() ,且BC=6,AD=AE=2CD=
,且BC=6,AD=AE=2CD=![]() .
.

(1)证明:AO⊥平面BCD;
(2)求二面角A-CD-B的平面角的正切值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD。在三角形OCD中,利用余弦定理求出OD,在三角形AOD中通过验证勾股定理可得AD⊥ OD.同理可得AO⊥OE。故可得出AO⊥ 平面BCD.(2)以O点为坐标原点,建立空间直角坐标系,求出平面ACD以及平面BCD的法向量。进而可得出二面角的余弦值以及正切值。
(1)证明易得 OC=3,连接OD,OE,在△OCD中,由余弦定理可得OD=![]() ,
,
因为AD=2![]() ,
,
所以AO2+OD2=AD2,所以AO⊥OD.
同理可证AO⊥OE,又OD∩OE=O,
所以AO⊥平面BCD.
(2)解以O点为原点,建立空间直角坐标系O-xyz(如图).
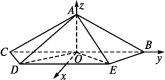
则A(0,0,![]() ),C(0,-3,0),D(1,-2,0),
),C(0,-3,0),D(1,-2,0),
所以![]() =(0,3,
=(0,3,![]() ),
),![]() =(-1,2,
=(-1,2,![]() ).
).
设n=(x,y,z)为平面ACD的法向量,
则
解得![]()
令x=1,得n=(1,-1,![]() ),
),
由(1)知,![]() =(0,0,
=(0,0,![]() )为平面CDB的一个法向量,
)为平面CDB的一个法向量,
所以cos<n,![]() >=
>=![]() ,
,
即二面角A'-CD-B的平面角的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,且
,且![]() 是奇函数,现给出下列4个结论:①
是奇函数,现给出下列4个结论:①![]() 是周期为4的周期函数;
是周期为4的周期函数;
②![]() 的图象关于点
的图象关于点![]() 对称;
对称;
③![]() 是偶函数;
是偶函数;
④![]() 的图象经过点
的图象经过点![]() ,其中正确结论的序号是__________(请填上所有正确的序号).
,其中正确结论的序号是__________(请填上所有正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左焦点为F,离心率为
=1(a>0,b>0)的左焦点为F,离心率为 ![]() .若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
A.![]()
=1
B.![]()
=1
C.![]()
=1
D.![]()
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为a的正方形,PA⊥平面ABCD.
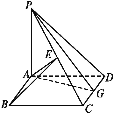
(1)若PA=AB,点E是PC的中点,求直线AE与平面PCD所成角的正弦值;
(2)若BE⊥PC且交点为E,BE=![]() a,G为CD的中点,线段AB上是否存在点F,使得EF∥平面PAG?若存在,求AF的长;若不存在,请说明理由.
a,G为CD的中点,线段AB上是否存在点F,使得EF∥平面PAG?若存在,求AF的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C截直线y=1所得线段的长度为2
,椭圆C截直线y=1所得线段的长度为2 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|.设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求∠EDF的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个顶点分别为A(﹣2,0),B(2,0),焦点在x轴上,离心率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4:5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者.(13分)
(1)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;
(2)从图中A,B,C,D四人中随机选出两人,记ξ为选出的两人中指标x的值大于1.7的人数,求ξ的分布列和数学期望E(ξ);
(3)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com