
【题目】若函数![]() 在其图象上存在不同的两点
在其图象上存在不同的两点![]() ,其坐标满足条件:
,其坐标满足条件:![]() 的最大值为0,则称
的最大值为0,则称![]() 为“柯西函数”,则下列函数:
为“柯西函数”,则下列函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中是“柯西函数”的为( )
.其中是“柯西函数”的为( )
A.①②B.③④C.①③D.②④
 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.
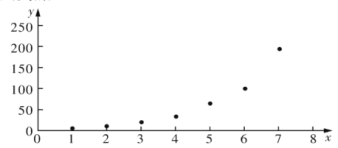
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次.
的回归方程,并预测活动推出第8天使用扫码支付的人次.
(3)推广期结束后,为更好的服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
人次 | 10 | 60 | 30 |
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调査结果发现:使用扫码支付的乘客中有5名乘客享受7折优惠,有10名乘客享受8折优惠,有15名乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: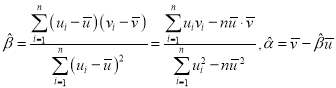 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面组成的多面体.如将正四面体所有棱各三等分,沿三等分点从原几何体割去四个小正四面体如图所示,余下的多面体就成为一个半正多面体,若这个半正多面体的棱长为2,则这个半正多面体的体积为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学设计一项综合学科的考查方案:考生从6道备选题中一次性随机抽取三道题,按照题目要求独立完成全部实验操作,已知在6道备选题中,考生甲有4道题能正确完成,两道题不能正确完成;考生乙每道题正确完成的概率都是![]() ,且每道题正确完成与否互不影响.
,且每道题正确完成与否互不影响.
(1)分别写出甲、乙两考生正确完成题数的概率分布列;
(2)分别求甲、乙两考生正确完成题数的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占80%.现从参与调查的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第1组
人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
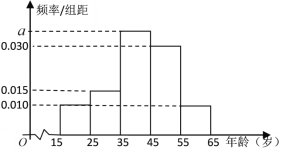
(1)求![]() 的值;
的值;
(2)求出样本的平均数(同一组数据用该区间的中点值作代表);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行问卷调查,求第2组中抽到
人进行问卷调查,求第2组中抽到![]() 人的概率.
人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)若曲线![]() 与
与![]() 只有一个公共点,求
只有一个公共点,求![]() 的值;
的值;
(2)![]() 为曲线
为曲线![]() 上的两点,且
上的两点,且![]() ,求
,求![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在悠久灿烂的中国古代文化中,数学文化是其中的一朵绚丽的奇葩.《张丘建算经》是我国古代有标志性的内容丰富的众多数学名著之一,大约创作于公元五世纪.书中有如下问题:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈,问日益几何?”.其大意为:“有一女子擅长织布,织布的速度一天比一天快,从第二天起,每天比前一天多织相同数量的布,第一天织![]() 尺,一个月共织了九匹三丈,问从第二天起,每天比前一天多织多少尺布?”.已知
尺,一个月共织了九匹三丈,问从第二天起,每天比前一天多织多少尺布?”.已知![]() 匹
匹![]() 丈,
丈,![]() 丈
丈![]() 尺,若这一个月有
尺,若这一个月有![]() 天,记该女子这一个月中的第
天,记该女子这一个月中的第![]() 天所织布的尺数为
天所织布的尺数为![]() ,
,![]() ,对于数列
,对于数列![]() 、
、![]() ,下列选项中正确的为( )
,下列选项中正确的为( )
A.![]() B.
B.![]() 是等比数列C.
是等比数列C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为
.斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() .若
.若![]() ,
,![]() 和点
和点![]() 共线,求
共线,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com