
【题目】已知正方体ABCD﹣A1B1C1D1中,点E是棱A1B1的中点,则直线AE与平面BDD1B1所成角的正弦值 . 
【答案】![]()
【解析】解:取AB的中点F,连接B1F,过点F作FG⊥BD,垂足为G,连接B1G,
由正方体性质易知BB1⊥平面ABCD,又FG平面ABCD,
∴BB1⊥FG
又FG⊥BD,BD∩BB1=B,BD平面BDD1B1 , BB1平面BDD1B1
∴FG⊥平面BDD1B1
∴∠FB1G为B1F与平面平面BDD1B1所成角
设正方体ABCD﹣A1B1C1D1棱长为1,
∴FG= ![]() ,B1F=
,B1F= ![]()
∴sin∠B1FO= 
而AE∥B1F,所以直线AE与平面BDD1B1所成角的正弦值为 ![]()
所以答案是: ![]()

【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则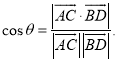 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】动点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,设
,设![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若点![]() 是
是![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() :
:![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 C:![]() 的焦距为2,且过点
的焦距为2,且过点![]() ,右焦点为
,右焦点为![]() .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为![]() ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
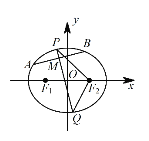
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() (
(![]() ,
,![]() )与椭圆C交于两点A、B,点D满足
)与椭圆C交于两点A、B,点D满足![]() ,经过点D及点
,经过点D及点![]() 的直线的斜率为
的直线的斜率为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图是函数y=Asin(ωx+φ)(x∈R)在区间 ![]() 上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( ) 
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
D.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c,cos2C+2 ![]() cosC+2=0.
cosC+2=0.
(1)求角C的大小;
(2)若b= ![]() a,△ABC的面积为
a,△ABC的面积为 ![]() sinAsinB,求sinA及c的值.
sinAsinB,求sinA及c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=![]() .
.
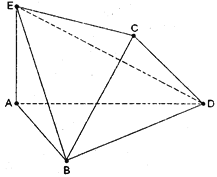
(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,若存在,求点M的位置,不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 袋中有形状、大小、质地完全一样的![]() 个红球和
个红球和![]() 个白球,从中随机抽出一个球,一定是红球
个白球,从中随机抽出一个球,一定是红球
B. 天气预报“明天降水概率![]() ”,是指明天有
”,是指明天有![]() 的时间会下雨
的时间会下雨
C. 某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票![]() 张,一定会中奖
张,一定会中奖
D. 连续掷一枚均匀硬币,若![]() 次都是正面朝上,则第六次仍然可能正面朝上
次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某山区养殖场散养的3500头猪中随机抽取5头,测量猪的体长x(cm)和体重y(kg),得如下测量数据:
猪编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 181 | 166 | 185 | 180 |
y | 95 | 100 | 97 | 103 | 101 |
(1)当且仅当x,y满足:x≥180且y≥100时,该猪为优等品,用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量;
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com