
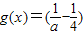 •
•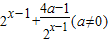 向左平移1个单位得到.
向左平移1个单位得到.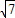 ,求实数a的取值范围.
,求实数a的取值范围.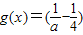 •
•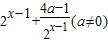 向左平移1个单位得到
向左平移1个单位得到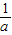 -
- )•2x+
)•2x+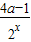
 •2x+
•2x+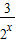 ≥2•
≥2•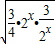 =3;
=3;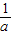 -
- )•2x•ln2+
)•2x•ln2+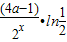
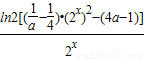 ,
,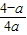 )•(2x)2>4a-1 ①
)•(2x)2>4a-1 ①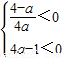 ,即a<0,时,(2x)2>
,即a<0,时,(2x)2>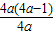 ,
,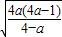 时,函数f(x)递增,
时,函数f(x)递增,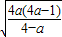 时,函数f(x)递减,
时,函数f(x)递减,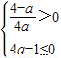 ,即0<a≤
,即0<a≤ 时,①式的解集为R,此时函数f(x)单调递增,
时,①式的解集为R,此时函数f(x)单调递增,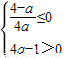 ,即a≥4时,①式的解集为∅.
,即a≥4时,①式的解集为∅.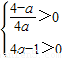 ,即
,即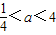 时,(2x)2>
时,(2x)2>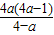 ,
,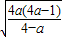 时,函数f(x)递增,
时,函数f(x)递增,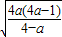 时,函数f(x)递减,
时,函数f(x)递减,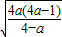 时,有最小值2
时,有最小值2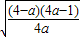 ,
,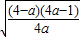 >
>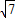 ,
, <a<2,
<a<2, ,2).
,2).

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com