
【题目】求下列不等式(组)的解集
(1)
(2)![]()
(3)求解关于![]() 的不等式
的不等式![]() ,其中
,其中![]() )
)
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合![]() 与
与![]() 的关系):
的关系):
年份代号( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
当年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)试预测2020年该企业的收入.
(参考公式: 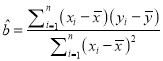
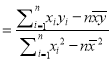 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ;
;
(1)讨论![]() 的极值点的个数;
的极值点的个数;
(2)若![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
参考数据:
| 1.6 | 1.7 | 1.8 |
| 4.953 | 5.474 | 6.050 |
| 0.470 | 0.531 | 0.588 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场预计全年分批购入电视机3600台,其中每台价值2000元,每批购入的台数相同,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入的电视机的总价值(不含运费)成正比,比例系数为![]() ,若每批购入400台,则全年需要支付运费和保管费共43600元.
,若每批购入400台,则全年需要支付运费和保管费共43600元.
(1)求![]() 的值;
的值;
(2)请问如何安排每批进货的数量,使支付运费与保管费的和最少?并求出相应最少费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,bsinA=![]() cosB.
cosB.
(1)求角B的大小;
(2)若b=2,△ABC的面积为![]() ,求a,c.
,求a,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问5分,(2)小问7分)
如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 过
过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]()

(1)若![]() ,求椭圆的标准方程
,求椭圆的标准方程
(2)若![]() 求椭圆的离心率
求椭圆的离心率![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com