
【题目】根据某地区气象水文部门长期统计,可知该地区每年夏季有小洪水的概率为0.25,有大洪水的概率为0.05.
(1)从该地区抽取的![]() 年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求
年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求![]() 的值;
的值;
(2)今年夏季该地区某工地有许多大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失20000元.为保护设备,有以下3种方案:
方案1:修建保护围墙,建设费为3000元,但围墙只能防小洪水.
方案2:修建保护大坝,建设费为7000元,能够防大洪水.
方案3:不采取措施.
试比较哪一种方案好,请说明理由.
【答案】(1)![]() ;(2)选择方案1好.
;(2)选择方案1好.
【解析】
(1)利用独立性重复试验二项分布概率计算公式列等量关系求![]() 的值;
的值;
(2)求出三种方案的期望值,对比选出期望值最小的方案.
(1)∵该地区每年夏季有小洪水的概率为0.25,有大洪水的概率为0.05
∴![]()
即该地区每年夏季无洪水的概率为![]() ,
,
∵该地区抽取的![]() 年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,且符合独立性重复试验二项分布,
年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,且符合独立性重复试验二项分布,
∴![]() ,
,
解得![]() ,
,
∴![]() ;
;
(2)设方案1、方案2和方案3的损失为随机变量为![]() 、
、![]() 和
和![]() ,分布列分别为:
,分布列分别为:
方案1
![]() ,
,![]() ,
,
| 3000 | 60000 |
| 0.95 | 0.05 |
∴![]() ,
,
方案2
![]()
| 7000 |
| 1 |
∴![]() ,
,
方案3
![]() ,
,![]() ,
,![]()
| 0 | 20000 | 60000 |
| 0.7 | 0.25 | 0.05 |
∴![]() ,
,
∴方案1的期望值最小,选择方案1好.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
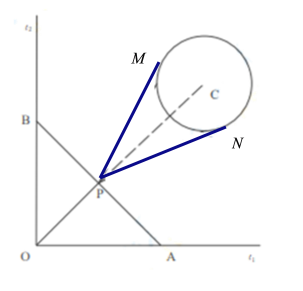
【题目】如图,在一旅游区内原有两条互相垂直且相交于点O的道路l1,l2,一自然景观的边界近似为圆形,其半径约为1千米,景观的中心C到l1,l2的距离相等,点C到点O的距离约为10千米.现拟新建四条游览道路方便游客参观,具体方案:在线段OC上取一点P,新建一条道路OP,并过点P新建两条与圆C相切的道路PM,PN(M,N为切点),同时过点P新建一条与OP垂直的道路AB(A,B分别在l1,l2上).为促进沿途旅游经济,新建道路长度之和越大越好,求新建道路长度之和的最大值.(所有道路宽度忽略不计)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的数列
的数列![]() 的首项
的首项![]() ,前n项和为
,前n项和为![]() ,若数列
,若数列![]() 满足:对任意正整数n,k,当
满足:对任意正整数n,k,当![]() 时,
时,![]() 总成立,则称数列
总成立,则称数列![]() 是“
是“![]() 数列”
数列”
(1)若![]() 是公比为2的等比数列,试判断
是公比为2的等比数列,试判断![]() 是否为“
是否为“![]() ”数列?
”数列?
(2)若![]() 是公差为d的等差数列,且是“
是公差为d的等差数列,且是“![]() 数列”,求实数d的值;
数列”,求实数d的值;
(3)若数列![]() 既是“
既是“![]() ”,又是“
”,又是“![]() ”,求证:数列
”,求证:数列![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() .过
.过![]() 三点的平面记为
三点的平面记为![]() ,
, ![]() 与
与![]() 的交点为
的交点为![]() .
.
(I)证明: ![]() 为
为![]() 的中点;
的中点;
(II)求此四棱柱被平面![]() 所分成上下两部分的体积之比.
所分成上下两部分的体积之比.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com