
(09年如东热身卷)(16分)设![]() 、
、![]()
![]() 是函数
是函数![]() 的两个极值点.
的两个极值点.
(I)若![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(II)若![]() ,求
,求![]() 的最大值;
的最大值;
(III)设函数![]() ,
,![]() ,当
,当![]() 时,
时,
求证:![]()
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
(09年如东热身卷)(10分)(10分)已知数列![]() 中,an=n(n+1)(n+2).又Sn=kn(n+1)(n+2)(n+3),试确定常数k,使S n恰为
中,an=n(n+1)(n+2).又Sn=kn(n+1)(n+2)(n+3),试确定常数k,使S n恰为![]() 的前n项的和,并用数学归纳法证明你的结论.
的前n项的和,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
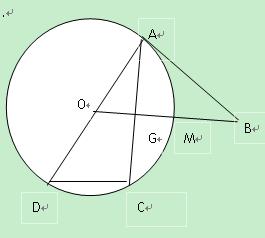
(09年如东热身卷)(10分)选修4-1几何证明选讲
如图,已知![]() 为圆O的直径,直线
为圆O的直径,直线![]() 与圆O相切于点
与圆O相切于点![]() ,直线
,直线![]() 与弦
与弦![]() 垂直并相交于点
垂直并相交于点![]() ,与弧
,与弧![]() 相交于
相交于![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com