
| f | �� n |
| f | �� 3 |
| ||
|
| fn(m) |
| fn+1(m) |
| f | �� 3 |
| ||
|
| fn(m) |
| fn+1(m) |
| n2 |
| x |
| n(xn-n) |
| x |
| n | n |
| n | n |
| n | n |
| n | n |
| n | n |
| n | n |
| n | n |
| n | n |
| fn��(x0) |
| fn-1��(x0) |
| fn(m) |
| fn-1(m) |
| nx0n-1 |
| (n+1)x0n |
| mn-1 |
| mn+1-1 |
| n(mn+1-1) |
| (n+1)(mn-1) |
| -mn+1+m(n+1)-n |
| (n+1)(mn-1) |


 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ln(x+n)-n |
| x+n |
| 1 |
| n(n+1) |
| x |
| ex-1 |
| 1 |
| en+1+e•n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| f2(x2)-f2(x1) | x2-x1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| f2(x2)-f2(x1) | x2-x1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012��㶫ʡ���ˮ����ѧ������ѧ�ڵ������¿��Ŀ���ѧ ���ͣ������
����С������14�֣���֪������ʵ�����ϵĺ���fn(x)=xn��n��N*���䵼������Ϊ ��������
��������
 ��a��x1��x2����,x1��x2��
��a��x1��x2����,x1��x2��
(1)����a��ֵ��
(2)�Ǻ���
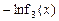 ��x�ʣ�0��e]����F(x)����СֵΪ6����ʵ��b��ֵ��
��x�ʣ�0��e]����F(x)����СֵΪ6����ʵ��b��ֵ��
(3)����(2)�е�b���躯�� ��A(x1��y1)��B(x2��y2)(x1<x2)�Ǻ���g(x)ͼ�������㣬��
��A(x1��y1)��B(x2��y2)(x1<x2)�Ǻ���g(x)ͼ�������㣬�� �����ж�x0��x1��x2�Ĵ�С��������֤����
�����ж�x0��x1��x2�Ĵ�С��������֤����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com