
【题目】(1)若数列![]() 的前n项和
的前n项和![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() .
.
(2)若数列![]() 的前n项和
的前n项和![]() ,证明
,证明![]() 为等比数列.
为等比数列.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)应用 ![]() (n
(n![]() ) 求解,再验证
) 求解,再验证![]() ,进而列出数列
,进而列出数列![]() 的通项公式
的通项公式![]() .
.
(2)应用 ![]() (n
(n![]() ) ,求得
) ,求得![]() 与bn-1的关系,进而证明
与bn-1的关系,进而证明 ![]() 为等比数列.
为等比数列.
(1) 当n≥2时,an=Sn-Sn-1=3n2-2n+1-[3(n-1)2-2(n-1)+1]=6n-5,
当n=1时,a1=S1=3×12-2×1+1=2;
显然当n=1时,不满足上式.
故数列的通项公式为![]()
(2)证明:由Tn=![]() bn+
bn+![]() ,得当n≥2时,Tn-1=
,得当n≥2时,Tn-1=![]() bn-1+
bn-1+![]() ,
,
两式相减,得bn=![]() bn-
bn-![]() bn-1,
bn-1,
∴当n≥2时,bn=-2bn-1,
又n=1时,T1=b1=![]() b1+
b1+![]() ,∴b1=1,
,∴b1=1,
∴bn=(-2)n-1.即![]() 为b1=1,公比q=-2的等比数列.
为b1=1,公比q=-2的等比数列.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】log0.72,log0.70.8,0.9﹣2的大小顺序是( )
A.log0.72<log0.70.8<0.9﹣2
B.log0.70.8<log0.72<0.9﹣2
C.0.9﹣2<log0.72<log0.70.8
D.log0.72<0.9﹣2<log0.70.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25. (Ⅰ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;
(Ⅱ)直线l的参数方程是 ![]() (t为参数),l与C交与A,B两点,|AB|=
(t为参数),l与C交与A,B两点,|AB|= ![]() ,求l的斜率.
,求l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)

男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试估计该公司职工每周平均上网时间超过4小时的概率是多少?
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的![]() 列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2-4ax+1+b(a>0)的定义域为[2,3],值域为[1,4];设g(x)=![]() .
.
(1)求a,b的值;
(2)若不等式g(2x)-k2x≥0在x∈[1,2]上恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知圆C过点P(1,1),且与圆M:![]() 关于直线
关于直线![]() 对称.
对称.
(1)求圆C的方程:
(2)设Q为圆C上的一个动点,求![]() 最小值;
最小值;
(3)过点P作两条相异直线分别与圆C交与A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP与直线AB是否平行?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为改善职工的出行条件,随机抽取50名职工,调查他们的居住地与公司的距离d(单位:千米).若样本数据分组为[0,2],(2,4],(4,6],(6,8],(8,10],(10,12],由数据绘制的分布频率直方图如图所示,则样本中职工居住地与公司的距离不超过4千米的人数为人. 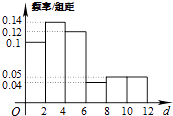
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]() .
.
(1)求函数f(x)的定义域和值域;
(2)设F(x)= ![]() [f2(x)﹣2]+f(x)(a为实数),求F(x)在a<0时的最大值g(a);
[f2(x)﹣2]+f(x)(a为实数),求F(x)在a<0时的最大值g(a);
(3)对(2)中g(a),若﹣m2+2tm+ ![]() ≤g(a)对a<0所有的实数a及t∈[﹣1,1]恒成立,求实数m的取值范围.
≤g(a)对a<0所有的实数a及t∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com