
【题目】命题![]() :关于
:关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,命题
,命题![]() :函数
:函数![]() 为增函数,分别求出符合下列条件的实数
为增函数,分别求出符合下列条件的实数![]() 的取值范围.
的取值范围.
(1)![]() 为真命题;
为真命题;
(2)“![]() ”为真,“
”为真,“![]() ”为假.
”为假.
【答案】(1)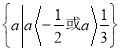 ;(2)
;(2)![]()
【解析】
试题一元二次不等式的二次项系数为正,说明抛物线的开口向上,不等式解集为空集,说明判别式小于0,解出命题p所表示的集合,指数函数为增函数说明底数大于1,解出命题q所表示的集合,若p或q为真命题,则p、q至少有一真,求出参数范围;“![]() ”为真,“
”为真,“![]() ”为假,说明p、q两个命题一真一假,分两种情况求出参数的范围.
”为假,说明p、q两个命题一真一假,分两种情况求出参数的范围.
试题解析:
命题p为真时,Δ=(a-1)2-4a2<0,即a>![]() 或a<-1.①命题q为真时,2a2-a>1,即a>1或a<-
或a<-1.①命题q为真时,2a2-a>1,即a>1或a<-![]() .②
.②
(1)当p∨q为真时,即p、q至少有一个是真命题,即上面两个范围的并集为![]() ;
;
∴“p∨q”为真时,a的取值范围是![]() .
.
(2)当“p∨q”为真,“p∧q”为假,即p,q有且只有一个是真命题时,有两种情况:当p真q假时,![]() <a≤1;当p假q真时,-1≤a<-
<a≤1;当p假q真时,-1≤a<-![]() .∴“p∨q”为真,“p∧q”为假时,a的取值范围是
.∴“p∨q”为真,“p∧q”为假时,a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
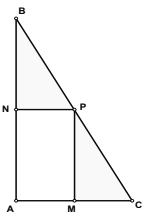
【题目】我校为丰富师生课余活动,计划在一块直角三角形![]() 的空地上修建一个占地面积为
的空地上修建一个占地面积为![]() (平方米)的
(平方米)的![]() 矩形健身场地,如图,点
矩形健身场地,如图,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() 点在斜边
点在斜边![]() 上,已知
上,已知![]() ,
, ![]() 米,
米, ![]() 米,
米, ![]() .设矩形
.设矩形![]() 健身场地每平方米的造价为
健身场地每平方米的造价为![]() 元,再把矩形
元,再把矩形![]() 以外(阴影部分)铺上草坪,每平方米的造价为
以外(阴影部分)铺上草坪,每平方米的造价为![]() 元(
元(![]() 为正常数)
为正常数)
(1)试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围;
的取值范围;
(2)求总造价![]() 关于面积
关于面积![]() 的函数
的函数![]() ;
;
(3)如何选取![]() ,使总造价
,使总造价![]() 最低(不要求求出最低造价)
最低(不要求求出最低造价)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 在
在![]() 处取极大值,在
处取极大值,在![]() 处取极小值.
处取极小值.
(1)若![]() ,求函数
,求函数![]() 的单调区间和零点个数;
的单调区间和零点个数;
(2)在方程![]() 的解中,较大的一个记为
的解中,较大的一个记为![]() ;在方程
;在方程![]() 的解中,较小的一个记为
的解中,较小的一个记为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最小值1,最大值9.
上有最小值1,最大值9.
(1)求实数a,b的值;
(2)设![]() ,若不等式
,若不等式![]() 在区间
在区间![]() 上恒成立,求实数k的取值范围;
上恒成立,求实数k的取值范围;
(3)设![]() ),若函数
),若函数![]() 有三个零点,求实数
有三个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级体育课举行了一次“投篮比赛”活动,为了了解本次投篮比赛学生总体情况,从中抽取了甲乙两个小组样本分数的茎叶图如图所示.
5 | 6 | 5 | 8 | ||||||
6 | 0 | 1 | 3 | 6 | 2 | 4 | 6 | 9 | |
7 | 1 | 2 | 7 | 1 | 3 | ||||
8 | 0 | 1 | 8 | 1 | |||||
甲 | 乙 | ||||||||
(1)分别求甲乙两个小组成绩的平均数与方差;
(2)分析比较甲乙两个小组的成绩;
(3)从甲组高于70分的同学中,任意抽取2名同学,求恰好有一名同学的得分在[80,90)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《聪明花开——莆仙话挑战赛》栏目共有五个项目,分别为“和一斗”“斗麻利”“文儒生”“放独步”“正功夫”.《聪明花开》栏目组为了解观众对项目的看法,设计了“你最喜欢的项目是哪一个”的调查问卷(每人只能选一个项目),对现场观众进行随机抽样调查,得到如下数据(单位:人):
和一斗 | 斗麻利 | 文儒生 | 放独步 | 正功夫 |
115 | 230 | 115 | 345 | 460 |
(1)在所有参与该问卷调查的人中,用分层抽样的方法抽取n人座谈,其中恰有4人最喜欢“斗麻利”,求n的值及所抽取的人中最喜欢“和一斗”的人数;
(2)在(1)中抽取的最喜欢“和一斗”和“斗麻利”的人中,任选2人参加栏目组互动,求恰有1人最喜欢“和一斗”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com