
【题目】某公园举办雕塑展览吸引着四方宾客,旅游人数![]() 与人均消费
与人均消费![]() (元)的关系如下:
(元)的关系如下: .
.
(1)若游客客源充足,那么当天接待游客多少人时,公园的旅游收入最多?
(2)若公园每天运营成本为5万元(不含工作人员的工资),还要上缴占旅游收入![]() 的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
【答案】(1)若游客客源充足,那么当天接待游客652人时,公园的旅游收入最多
(2)要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在520人到778人之间
【解析】
(1)根据旅游收入![]() 旅游人数
旅游人数![]() 人均消费,把旅游人数
人均消费,把旅游人数![]() 与人均消费
与人均消费![]() 的分段函数式代入计算即可;
的分段函数式代入计算即可;
(2)考虑公园每天运营的最低成本为![]() ,可排除第一种情况;第二种情况应满足:旅游收入
,可排除第一种情况;第二种情况应满足:旅游收入![]() ,求出
,求出![]() 的范围,从而得出旅游人数
的范围,从而得出旅游人数![]() 的范围.
的范围.
(1)设当天的旅游收入为![]() ,那么
,那么![]() ,
,
得 ;
;
当![]() 时,
时,![]() (元
(元![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() 当
当![]() 元时,
元时,![]() (元
(元![]() ,此时
,此时![]() (人
(人![]() ,
,
故当天接待旅游人数为652人时旅游收入最多,最多收入为70416元;
(2)要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营,
则每天的旅游收入上缴税收后应不低于![]() 元,
元,
因![]() ,
,![]() ,显然不满足条件;
,显然不满足条件;
故由![]() ,得
,得![]() ,
,
又![]() ,解得
,解得![]() ;
;
此时旅游人数![]() 满足:
满足:![]() ,
,
故每天的游客人数应控制在520人到778人之间.


科目:高中数学 来源: 题型:
【题目】如图所示的几何体,关于其结构特征,下列说法不正确的是
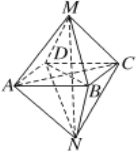
A. 该几何体是由两个同底的四棱锥组成的几何体
B. 该几何体有12条棱、6个顶点
C. 该几何体有8个面,并且各面均为三角形
D. 该几何体有9个面,其中一个面是四边形,其余均为三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋有![]() 个白球,
个白球,![]() 个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为
个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为![]() ,
,![]() ,
,![]() ,
,![]() 的抽屉内.
的抽屉内.
(1)求编号为![]() 的抽屉内放黑球的概率;
的抽屉内放黑球的概率;
(2)口袋中的球放入抽屉后,随机取出两个抽屉中的球,求取出的两个球是一黑一白的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分) 如图,![]() 的外接圆
的外接圆![]() 的半径为
的半径为![]() ,
,![]() 所在的平面,
所在的平面,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
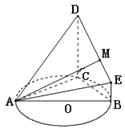
(1)求证:平面ADC![]() 平面BCDE.
平面BCDE.
(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为![]() ?若存在,
?若存在,
确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)已知中心在原点O,焦点在x轴上,离心率为![]() 的椭圆过点(
的椭圆过点(![]() ,
,![]() ).
).
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.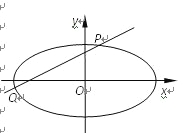
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的是( )
A.半圆弧以其直径为轴旋转一周所形成的曲面叫做球
B.直角三角形绕一直角边为轴旋转一周得到的旋转体是圆锥
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体
D.用一个平面截圆锥底面与截面组成的部分是圆台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() 。数列
。数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 。
。
(1)求数列![]() 的通项公式及其前
的通项公式及其前![]() 项和
项和![]() ;
;
(2)证明数列![]() 为等差数列,并求出
为等差数列,并求出![]() 的通项公式;
的通项公式;
(3)设数列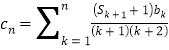 ,问是否存在正整数
,问是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列,若存在,求出所有满足要求的
成等差数列,若存在,求出所有满足要求的![]() ;若不存在,请说明理由。
;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知动点![]() 都在曲线
都在曲线![]() (
(![]() 为参数,
为参数,![]() 是与
是与![]() 无关的正常数)上,对应参数分别为
无关的正常数)上,对应参数分别为![]() 与
与![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)作一个伸压变换:![]() ,求出动点
,求出动点![]() 点的参数方程,并判断动点
点的参数方程,并判断动点![]() 的轨迹能否过点
的轨迹能否过点![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com