
| 参加书法班 | 未参加书法班 | |
| 参加演讲班 | 8 | 5 |
| 未参加演讲班 | 2 | 33 |
分析 (I)由调查数据可知,既未参加书法班又未参加演讲班的有33人,故至少参加上述一个班的共有48-33=15人,由此能求出从该老年大学随机选1名学员,该学员至少参加上述一个班的概率.
(II)从这5名男学员和3名女学员中各随机选1人,其一切的可能结果组成的基本事件有n=5×3=15个,再用列举法求出事件“A1被选中且B1未被选中”所包含的基本事件的个数,由此能求出A1被选中且B1未被选中的概率.
解答 解:(I)由调查数据可知,既未参加书法班又未参加演讲班的有33人,
故至少参加上述一个班的共有48-33=15人,
所以从该老年大学随机选1名学员,
该学员至少参加上述一个班的概率为$p=\frac{15}{48}=\frac{5}{16}$.(4分)
(II)从这5名男学员和3名女学员中各随机选1人,
其一切的可能结果组成的基本事件有n=5×3=15个,
根据题意,这些基本事件的出现是等可能的,
事件“A1被选中且B1未被选中”所包含的基本事件有{A1,B2},{A1,B3}共2个.
因此,A1被选中且B1未被选中的概率为p=$\frac{2}{15}$.(10分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
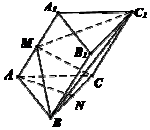 如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.
如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com