已知f的函数．对任意两个不相等的正数x1.x2.都有$\frac{{x} {2}f-{x} {1}f}{{x} {1}-{x} {2}}$＞0.记a=$\frac{f}{{3}^{0.2}}$.b=$\frac{f}{0．{3}^{2}}$.c=$\frac{f}{lo{g} {2}5}$.则( )A．a＜b＜cB．b＜a＜cC．c＜a＜bD．c＜b＜a 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

1．已知f（x）是定义在（0，+∞）的函数．对任意两个不相等的正数x₁，x₂，都有$\frac{{x}_{2}f（{x}_{1}）-{x}_{1}f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0，记a=$\frac{f（{3}^{0.2}）}{{3}^{0.2}}$，b=$\frac{f（0．{3}^{2}）}{0．{3}^{2}}$，c=$\frac{f（lo{g}_{2}5）}{lo{g}_{2}5}$，则（　　）

A．

a＜b＜c

B．

b＜a＜c

C．

c＜a＜b

D．

c＜b＜a

分析由题意可得函数$\frac{f（x）}{x}$是（0，+∞）上的增函数，比较大小可得0.3²＜3^0.2＜log₂5，故可得答案．

解答解：∵f（x）是定义在（0，+∞）上的函数，对任意两个不相等的正数x₁，x₂，都有$\frac{{x}_{2}f（{x}_{1}）-{x}_{1}f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0，
∴函数$\frac{f（x）}{x}$是（0，+∞）上的增函数，
∵1＜3^0.2＜3，0＜0.3²＜1，log₂5＞2，
∴0.3²＜3^0.2＜log₂5，
∴b＜a＜c．
故选：B．

点评本题主要考查利用函数的单调性比较大小，考查学生对指数函数、对数函数性质的运用能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

11．

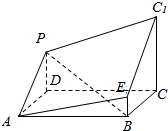如图所示的多面体是由底面为ABCD的长方体被截面AEC₁F所截得到的，其中AB=4，BC=2，CC₁=3，BE=1，则点F到平面AEC的距离为（　　）

A．

$\frac{1}{7}$

B．

$\frac{\sqrt{21}}{7}$

C．

$\frac{4\sqrt{21}}{7}$

D．

$\frac{8}{7}$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．对函数f（x）=$\sqrt{3}sinxcosx+{cos}^{2}x-\frac{1}{2}$的表述错误的是（　　）

	A．	最小正周期为π
	B．	函数y=sin2x向左平移$\frac{π}{12}$个单位可得到f（x）
	C．	f（x）在区间$（-\frac{π}{3}，\frac{π}{6}）$上递增
	D．	点$（\frac{π}{6}，0）$是f（x）的一个对称中心

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．（Ⅰ）若集合A={-1，2，4，6}，B={x|x=m²-1，m∈A}，请用列举法表示集合B；
（Ⅱ）已知集合 $A=\left\{{a，\;\frac{b}{a}，\;b+1}\right\}$，B={a²，a，0}，且A=B，计算a，b的值；
（Ⅲ）已知全集U=R，集合A={x|log₂x≤2}，B={x|-2≤x≤3}求：A∩∁_UB．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

16．已知2^m=9ⁿ=6，$\frac{1}{m}+\frac{1}{2n}$=1．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．对定义在R上的函数f（x），若实数x₀满足f（x₀）=x₀，则x₀称为f（x）的一个不动点．设二次函数f（x）=x²+mx-m+2，若f（x）在[0，+∞）上有不动点，则m的取值范围是（　　）

A．

[-1-2$\sqrt{2}$，2]

B．

（-∞，-1-2$\sqrt{2}$]∪[2，+∞）

C．

[-1，2]