
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)过![]() 作截面与线段
作截面与线段![]() 交于点H,使得
交于点H,使得![]() 平面
平面![]() ,试确定点H的位置,并给出证明;
,试确定点H的位置,并给出证明;
(2)在(1)的条件下,若二面角![]() 的大小为
的大小为![]() ,试求直线
,试求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)H为线段![]() 上靠近点P的五等分点,即
上靠近点P的五等分点,即![]() ,证明见解析;(2)
,证明见解析;(2)![]()
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() .证明
.证明![]() ,即可证明
,即可证明![]() 平面
平面![]() .
.
(2)以![]() ,
,![]() 为x,y轴的正方向,过点D作平面
为x,y轴的正方向,过点D作平面![]() 的垂线为z轴建立空间直角坐标系,求出平面
的垂线为z轴建立空间直角坐标系,求出平面![]() 的法向量,利用空间向量的数量积求解直线
的法向量,利用空间向量的数量积求解直线![]() 与平面
与平面![]() 所成角的正弦值即可.
所成角的正弦值即可.
(1)如图,连接![]() 交
交![]() 于点E,
于点E,

由![]() ,易知
,易知![]() 相似于
相似于![]() .
.
∴![]() ,
,
又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∴![]() ,即H为线段
,即H为线段![]() 上靠近点P的五等分点,即
上靠近点P的五等分点,即![]() .
.
(2)由![]() ,
,![]() 相似于
相似于![]() ,可得
,可得![]() ,
,
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角,∵
的平面角,∵![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,![]() ,
,
又易知![]() ,∴
,∴![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量,
的法向量,
如图,以![]() ,
,![]() 为x,y轴的正方向,过点D作平面
为x,y轴的正方向,过点D作平面![]() 的垂线为z轴建立空间直角坐标系,
的垂线为z轴建立空间直角坐标系,

则![]() ,
,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴ ,直线
,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】圆周上有![]() 个白点,先将其中一个染为黑色(称为第一次染色),对任何正整数
个白点,先将其中一个染为黑色(称为第一次染色),对任何正整数![]() ,第
,第![]() 次染色后按逆时针方向间隔
次染色后按逆时针方向间隔![]() 个点将下个点染成与原来颜色相反的颜色(称为第
个点将下个点染成与原来颜色相反的颜色(称为第![]() 次染色).
次染色).
(1)对给定正整数![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 次染色后
次染色后![]() 个点均为白色?
个点均为白色?
(2)对给定正整数![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 次染色后
次染色后![]() 个点均为黑色?
个点均为黑色?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2014-2018年的相关数据如下表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数 | 2 | 4 | 5 | 6 | 8 |
该产品的年利润 | 30 | 40 | 60 | 50 | 70 |
年返修台数(台) | 19 | 58 | 45 | 71 | 70 |
注:![]()
(1)从该公司2014-2018年的相关数据中任意选取3年的数据,求这3年中至少有2年生产部门考核优秀的概率.
(2)利用上表中五年的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的回归直线方程是
(万台)的回归直线方程是![]() ①.现该公司计划从2019年开始转型,并决定2019年只生产该产品1万台,且预计2019年可获利32(百万元);但生产部门发现,若用预计的2019年的数据与2014-2018年中考核优秀年份的数据重新建立回归方程,只有当重新估算的
①.现该公司计划从2019年开始转型,并决定2019年只生产该产品1万台,且预计2019年可获利32(百万元);但生产部门发现,若用预计的2019年的数据与2014-2018年中考核优秀年份的数据重新建立回归方程,只有当重新估算的![]() ,
,![]() 的值(精确到0.01),相对于①中
的值(精确到0.01),相对于①中![]() ,
,![]() 的值的误差的绝对值都不超过
的值的误差的绝对值都不超过![]() 时,2019年该产品返修率才可低于千分之一.若生产部门希望2019年考核优秀,能否同意2019年只生产该产品1万台?请说明理由.
时,2019年该产品返修率才可低于千分之一.若生产部门希望2019年考核优秀,能否同意2019年只生产该产品1万台?请说明理由.
(参考公式:![]() ,
,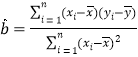
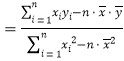 ,
,![]() ,
,![]() 相对
相对![]() 的误差为
的误差为![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X(40≤X<200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:
蔬菜量X | [40,80) | [80,120) | [120,160) | [160,200) |
天数 | 25 | 50 | 100 | 25 |
若将频率视为概率,试解答如下问题:
(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;
(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 为抛物线
为抛物线![]() 上的两点,
上的两点,![]() 与
与![]() 的中点的纵坐标为4,直线
的中点的纵坐标为4,直线![]() 的斜率为
的斜率为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,
,![]() 、
、![]() 为抛物线
为抛物线![]() (除原点外)上的不同两点,直线
(除原点外)上的不同两点,直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且满足
,且满足![]() ,记抛物线
,记抛物线![]() 在
在![]() 、
、![]() 处的切线交于点
处的切线交于点![]() ,若点
,若点![]() 、
、![]() 的中点的纵坐标为8,求点
的中点的纵坐标为8,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
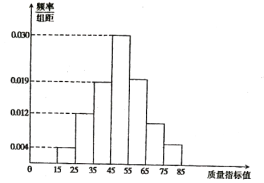
(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)用分层抽样的方法在区间![]() 内抽取一个容量为
内抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任意抽取
的样本,将该样本看成一个总体,从中任意抽取![]() 件桥梁构件,求这
件桥梁构件,求这![]() 件桥梁构件都在区间
件桥梁构件都在区间![]() 内的概率
内的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com