
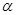 、
、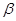 和直线
和直线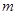 ,给出条件:①
,给出条件:①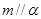 ;②
;②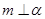 ;③
;③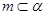 ;④
;④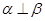 ;⑤
;⑤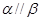 .
.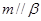 的是( )
的是( )| A.①④ | B.①⑤ | C.②⑤ | D.③⑤ |
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源:不详 题型:解答题
 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.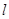 ,求证:
,求证: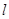 ∥平面BCDE;
∥平面BCDE;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
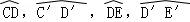 的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.
的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.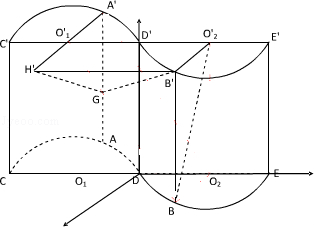
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中, 四边形
中, 四边形 是正方形,
是正方形, ,
, .将正方形沿
.将正方形沿 折起,得到如图2所示的多面体,其中面
折起,得到如图2所示的多面体,其中面 面
面 ,
, 是
是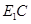 中点.
中点. ∥平面
∥平面 ;
; 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求AB和CD所成角的余弦值.
,求AB和CD所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com