
【题目】设数列![]() 前n项和为
前n项和为![]() ,且
,且![]() 其中m为实常数,
其中m为实常数,![]() 且
且![]() .
.
(1)求证:![]() 是等比数列;
是等比数列;
(2)若数列![]() 的公比满足
的公比满足![]() 且
且![]() ,
,![]() ,求证:数列
,求证:数列![]() 是等差数列,并求
是等差数列,并求![]() 的通项公式;
的通项公式;
(3)若![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n和
的前n和![]() .
.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民健身倡导全民做到每天参加一次以上的体育健身活动,旨在全面提高国民体质和健康水平.某部门在该市2013-2018年发布的全民健身指数中,对其中的“运动参与评分值![]() ”(满分100分)进行了统计,制成如图所示的散点图.
”(满分100分)进行了统计,制成如图所示的散点图.
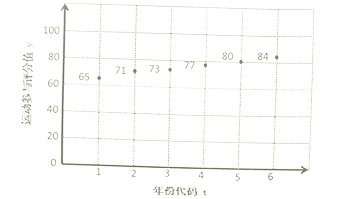
(1)根据散点图,建立![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)从该市的市民中随机抽取了容量为150的样本,其中经常参加体育锻炼的人数为50,以频率为概率,若从这150名市民中随机抽取4人,记其中“经常参加体育锻炼”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为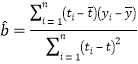 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列4个命题:
①若函数![]() 在
在![]() 上有零点,则一定有
上有零点,则一定有![]() ;
;
②函数![]() 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数;
③若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④若函数![]() 满足条件
满足条件![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确命题的序号是:_______.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对边分别为a、b、c,且2acosC=2b-c.
(1)求角A的大小;
(2)若AB=3,AC边上的中线SD的长为![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com