
分析 (1)由对数的运算性质得到0<log${\;}_{\frac{1}{3}}$x<3,再由对数的运算性质得答案;
(2)由根式${a}^{lo{g}_{a}b}=b$把原不等式化为二次不等式组,求解不等式组得答案.
解答 解:(1)由log3(log${\;}_{\frac{1}{3}}$x)<1,
得0<log${\;}_{\frac{1}{3}}$x<3,即$\frac{1}{27}<x<1$.
∴不等式log3(log${\;}_{\frac{1}{3}}$x)<1 的解集为($\frac{1}{27},1$);
(2)由($\frac{1}{3}$)${\;}^{lo{g}_{\frac{1}{3}}({x}^{2}-3x-10)}$≤27,
得0<x2-3x-10≤27,即
$\left\{\begin{array}{l}{{x}^{2}-3x-10>0}\\{{x}^{2}-3x-10≤27}\end{array}\right.$,解得:$\frac{3-\sqrt{157}}{2}≤x<-2$或5$<x≤\frac{3+\sqrt{157}}{2}$.
∴不等式($\frac{1}{3}$)${\;}^{lo{g}_{\frac{1}{3}}({x}^{2}-3x-10)}$≤27的解集为$[\frac{3-\sqrt{157}}{2},-2)$∪$(5,\frac{3+\sqrt{157}}{2}]$.
点评 本题考查指数不等式和对数不等式的解法,关键是熟记对数的运算性质,考查计算能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
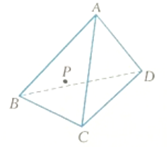 如图,一个四面体木块ABCD,在△ABC的面内有一点P,要经过点P在平面ABC内画一条直线l,使l⊥AD,怎样画?写出作法,并给予证明.
如图,一个四面体木块ABCD,在△ABC的面内有一点P,要经过点P在平面ABC内画一条直线l,使l⊥AD,怎样画?写出作法,并给予证明.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | bc<ad | B. | bc>ad | C. | $\frac{a}{c}$$<\frac{1}{b}$ | D. | $\frac{a}{c}$$<\frac{b}{d}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com