【题目】某商场预计全年分批购入每台2000元的电视机共3600台．每批都购入
台（是自然数）且每批均需付运费400元．贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值（不含运费）成正比．若每批购入400台，则全年需用去运输和保管总费用43600元．现在全年只有24000元资金可以支付这笔费用，请问，能否恰当安排每批进货数量，使资金够用？写出你的结论，并说明理由．
互动英语系列答案科目：高中数学 来源： 题型：
【题目】设
为数列
的前
项和，对任意的
，都有
（
为正常数）.
（1）求证：数列
是等比数列；
（2）数列
满足
，
，求数列
的通项公式；
（3）在满足（2）的条件下，求数列
的前
项和
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）如图，点A，B是单位圆上的两点，A，B两点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，若点A的坐标为（
，
），记∠COA＝α．
（Ⅰ）求
的值；
（Ⅱ）求cos∠COB的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，三棱柱
的侧面
是边长为1的正方形，侧面
侧面
是
的中点．
（1）求证：
平面
；
（2）求证：
平面
；
（3）在线段
上是否存在一点
，使二面角
为45°，若存在，求
的长；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】铁矿石A和B的含铁率为
,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
的价格c如下表：
| b(万吨) |
| |
A | 50% | 1 | 3 |
B | 70% | 0．5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元)．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了弘扬民族文化，某校举行了“我爱国学，传诵经典”考试，并从中随机抽取了100名考生的成绩（得分均为整数，满分100分）进行统计制表，其中成绩不低于80分的考生被评为优秀生，请根据频率分布表中所提供的数据，用频率估计概率，回答下列问题．
分组 | 频数 | 频率 |
| 5 |
|
|
|
|
| 35 |
|
| 25 |
|
| 15 |
|
合计 | 100 |
|
（Ⅰ）求
的值及随机抽取一考生恰为优秀生的概率；
（Ⅱ）按成绩采用分层抽样抽取20人参加学校的“我爱国学”宣传活动，求其中优秀生的人数；
（Ⅲ）在第（Ⅱ）问抽取的优秀生中指派2名学生担任负责人，求至少一人的成绩在
的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C： 
，直线l： 
（Ⅰ）求直线l所过定点A的坐标；
（Ⅱ）求直线l被圆C所截得的弦长最短时m的值及最短弦长；
（Ⅲ）已知点
，在直线MC上（C为圆心），存在定点N（异于点M），满足：对于圆C上任一点P，都有
为一常数，试求所有满足条件的点N的坐标及该常数。
查看答案和解析>>
科目：高中数学 来源： 题型：
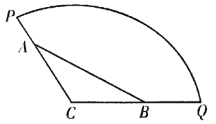
【题目】为方便市民休闲观光，市政府计划在半径为200
，圆心角为
的扇形广场内（如图所示），沿△
边界修建观光道路，其中
、
分别在线段
、
上，且
、
两点间距离为定长
．
（1）当
时，求观光道
段的长度；
（2）为提高观光效果，应尽量增加观光道路总长度，试确定图中
、
两点的位置，使观光道路总长度达到最长？并求出总长度的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从
中这
个数中取
个数组成递增等差数列，所有可能的递增等差数列这个数记为
.
（1）当
时，写出所有可能的递增等差数列及
的值；
（2）求
；
（3）求证:
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
