解:(1)∵点P在函数y=f(x)上,由f(x)=

mx
2-2x+1+ln(x+1)(m≥1);
得:f′(x)=mx-2+

(m≥1);
∴y′|
x=0=-1 故切线方程为:y=-x+1…(3分)
(2)由g(x)=f(x)+x-1=

mx
2-x+ln(x+1),
可知:定义域为(-1,+∞),且g(0)=0,显然x=0为y=g(x)的一个零点;
则g′(x)=mx-1+

…(5分)
①当m=1时,g′(x)=
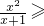
0,即函数y=g(x)在(-1,+∞)上单调递增,g(0)=0,故仅有一个零点,满足题意.…(6分)
②当m>1时,则
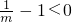
,列表分析:
| x | (-1,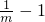 ) ) | 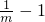 | (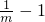 ,0) ,0) | 0 | (0,+∞) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | 增 | 极大值
g(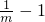 ) ) | 减 | 极小值
0 | 增 |
又∵x→-1时,g(x)→-∞,∴g(x)在(-1,
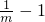
)上有一根,这与y=g(x)仅有一根矛盾,
故此种情况不符题意.…(9分)
(3)假设y=f(x)存在单调区间,由f(x)=

mx
2-2x+1+ln(x+1)(m≥1);
f(x)=得:f′(x)=mx-2+

=
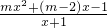
,…(10分)
令h(x)=mx
2+(m-2)x-1,∵△=m
2+4>0,h(-1)=m+2-m-1=1>0,
∴h(x)=0在(-1,+∞)上一定存在两个不同的实数根s,t,…(12分)
即h(x)=mx
2+(m-2)x-1<0的解集为(t,s),即函数f(x)存在单调区间[t,s],
则s-t=
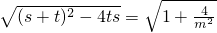
,由m≥1可得:s-t∈(1,

]…(14分)
分析:(1)根据导数的几何意义求出函数f(x)在x=0处的导数,从而求出切线的斜率,再用点斜式写出切线方程即可;
(2)先写出g(x)的解析式,可知g(0)=0,显然x=0为y=g(x)的一个零点;再利用导数g′(x)=mx-1+

研究函数y=g(x)在(-1,+∞)上单调性,从而求出m的值;
(3)对于存在性问题,可先假设存在,即假设y=f(x)存在单调区间,再利用导数工具研究函数的单调区间,求出s-t的取值范围,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:本题考查了导数的几何意义及利用导数研究函数的单调性的处理策略,解题时,弄清题意,合理运用导数工具的处理策略是关键

 mx2-2x+1+ln(x+1)(m≥1);
mx2-2x+1+ln(x+1)(m≥1); mx2-2x+1+ln(x+1)(m≥1);
mx2-2x+1+ln(x+1)(m≥1); (m≥1);
(m≥1); mx2-x+ln(x+1),
mx2-x+ln(x+1), …(5分)
…(5分)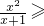 0,即函数y=g(x)在(-1,+∞)上单调递增,g(0)=0,故仅有一个零点,满足题意.…(6分)
0,即函数y=g(x)在(-1,+∞)上单调递增,g(0)=0,故仅有一个零点,满足题意.…(6分)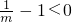 ,列表分析:
,列表分析: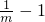 )
)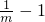
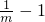 ,0)
,0)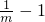 )
)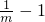 )上有一根,这与y=g(x)仅有一根矛盾,
)上有一根,这与y=g(x)仅有一根矛盾, mx2-2x+1+ln(x+1)(m≥1);
mx2-2x+1+ln(x+1)(m≥1); =
=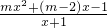 ,…(10分)
,…(10分)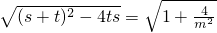 ,由m≥1可得:s-t∈(1,
,由m≥1可得:s-t∈(1, ]…(14分)
]…(14分) 研究函数y=g(x)在(-1,+∞)上单调性,从而求出m的值;
研究函数y=g(x)在(-1,+∞)上单调性,从而求出m的值;
