
【题目】已知函数f(x)=sin2x﹣cos2x﹣2![]() sinx cosx(x∈R).
sinx cosx(x∈R).
(Ⅰ)求f(![]() )的值.
)的值.
(Ⅱ)求f(x)的最小正周期及单调递增区间.
【答案】(Ⅰ)2.(Ⅱ)最小正周期为π,单调递增区间[kπ+![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.
【解析】试题分析:(Ⅰ)把集合B化简后,由A∩B=,A∪B=R,借助于数轴列方程组可解a的值;(Ⅱ)把p是q的充分条件转化为集合A和集合B之间的关系,运用两集合端点值之间的关系列不等式组求解a的取值范围.
试题解析:解:∵函数f(x)=sin2x﹣cos2x﹣2![]() sinx cosx=﹣
sinx cosx=﹣![]() sin2x﹣cos2x=2sin(2x+
sin2x﹣cos2x=2sin(2x+![]() )
)
(Ⅰ)f(![]() )=2sin(2×
)=2sin(2×![]() +
+![]() )=2sin
)=2sin![]() =2,
=2,
(Ⅱ)∵ω=2,故T=π,
即f(x)的最小正周期为π,
由2x+![]() ∈[﹣
∈[﹣![]() +2kπ,
+2kπ,![]() +2kπ],k∈Z得:
+2kπ],k∈Z得:
x∈[﹣![]() +kπ,﹣
+kπ,﹣![]() +kπ],k∈Z,
+kπ],k∈Z,
故f(x)的单调递增区间为[﹣![]() +kπ,﹣
+kπ,﹣![]() +kπ]或写成[kπ+
+kπ]或写成[kπ+![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.


科目:高中数学 来源: 题型:
【题目】.(本小题满分14分)已知等比数列![]() 的公比为
的公比为![]() ,首项为
,首项为![]() ,其前
,其前![]() 项的和为
项的和为![]() .数列
.数列![]() 的前
的前![]() 项的和为
项的和为![]() , 数列
, 数列![]() 的前
的前![]() 项的和为
项的和为![]()
(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当![]() 为奇数时,比较
为奇数时,比较![]() 与
与![]() 的大小; ②当
的大小; ②当![]() 为偶数时,若
为偶数时,若![]() ,问是否存在常数
,问是否存在常数![]() (与n无关),使得等式
(与n无关),使得等式![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点. 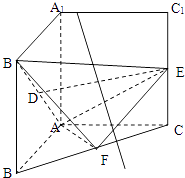
(1)求证:DE∥平面ABC;
(2)求证:B1F⊥平面AEF;
(3)求二面角A﹣EB1﹣F的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
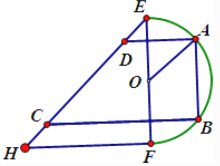
【题目】为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆![]() 及等腰直角三角形
及等腰直角三角形![]() ,其中
,其中![]() ,为裁剪出面积尽可能大的梯形铁片
,为裁剪出面积尽可能大的梯形铁片![]() (不计损耗),将点
(不计损耗),将点![]() 放在弧
放在弧![]() 上,点
上,点![]() 放在斜边
放在斜边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)求梯形铁片![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试确定![]() 的值,使得梯形铁片
的值,使得梯形铁片![]() 的面积
的面积![]() 最大,并求出最大值.
最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国移动通信公司早前推出“全球通”移动电话资费“个性化套餐”,具体方案如下:
方案代号 | 基本月租(元) | 免费时间(分钟) | 超过免费时间的话费(元/分钟) |
1 | 30 | 48 | 0.60 |
2 | 98 | 170 | 0.60 |
3 | 168 | 330 | 0.50 |
4 | 268 | 600 | 0.45 |
5 | 388 | 1000 | 0.40 |
6 | 568 | 1700 | 0.35 |
7 | 788 | 2588 | 0.30 |
(I)写出“套餐”中方案![]() 的月话费
的月话费![]() (元)与月通话量
(元)与月通话量![]() (分钟)(月通话量是指一个月内每次通话用时之和)的函数关系式;
(分钟)(月通话量是指一个月内每次通话用时之和)的函数关系式;
(II)学生甲选用方案![]() ,学生乙选用方案
,学生乙选用方案![]() ,某月甲乙两人的电话资费相同,通话量也相同,求该月学生甲的电话资费;
,某月甲乙两人的电话资费相同,通话量也相同,求该月学生甲的电话资费;
(III)某用户的月通话量平均为320分钟,则在表中所列出的七种方案中,选择哪种方案更合算,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com