
已知平面区域 由以
由以 、
、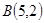 、
、 为顶点的三角形内部和边界组成.若在区域
为顶点的三角形内部和边界组成.若在区域 上有无穷多个点
上有无穷多个点 可使目标函数
可使目标函数 取得最小值,则
取得最小值,则 ( )
( )







C
解析考点:简单线性规划的应用.
专题:数形结合.
分析:将目标函数z=x+my化成斜截式方程后得:y="-"  x+
x+  z,若m>0时,目标函数值Z与直线族:y="-"
z,若m>0时,目标函数值Z与直线族:y="-"  x+
x+  z截距同号,当直线族y="-"
z截距同号,当直线族y="-"  x+
x+  z的斜率与直线AC的斜率相等时,目标函数z=x+my取得最小值的最优解有无数多个;若m<0时,目标函数值Z与直线族:y="-"
z的斜率与直线AC的斜率相等时,目标函数z=x+my取得最小值的最优解有无数多个;若m<0时,目标函数值Z与直线族:y="-"  x+
x+  z截距异号,当直线族y="-"
z截距异号,当直线族y="-"  x+
x+  z的斜率与直线BC的斜率相等时,目标函数z=x+my取得最小值的最优解有无数多个.但由于AC与BC的斜率为负,则不满足第二种情况,由此不难得到m的值.
z的斜率与直线BC的斜率相等时,目标函数z=x+my取得最小值的最优解有无数多个.但由于AC与BC的斜率为负,则不满足第二种情况,由此不难得到m的值.
解答:解:依题意,令z=0,可得直线x+my=0的斜率为- ,
,
结合可行域可知当直线x+my=0与直线AC平行时,
线段AC上的任意一点都可使目标函数z=x+my取得最小值,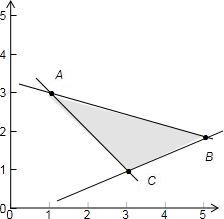
而直线AC的斜率为-1,所以m=1.
故答案为:1.
点评:目标函数的最优解有无数多个,处理方法一般是:①将目标函数的解析式进行变形,化成斜截式②分析Z与截距的关系,是符号相同,还是相反③根据分析结果,结合图形做出结论④根据斜率相等求出参数.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源:2010-2011年河北冀州中学高一年级下学期期末考试文科数学(B卷) 题型:单选题
已知平面区域 由以
由以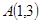 、
、 、
、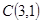 为顶点的三角形内部和边界组成.若在区域
为顶点的三角形内部和边界组成.若在区域 上有无穷多个点
上有无穷多个点 可使目标函数
可使目标函数 取得最小值,则
取得最小值,则 ( )
( )







查看答案和解析>>
科目:高中数学 来源:2015届江西南昌八一、中学、麻丘中学高二10月联考数学卷(解析版) 题型:选择题
已知平面区域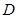 由以
由以 、
、 、
、 为顶点的三角形内部和边界组成.若在区域
为顶点的三角形内部和边界组成.若在区域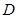 上有无穷多个点
上有无穷多个点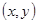 可使目标函数
可使目标函数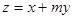 取得最小值,则
取得最小值,则 ( )
( )
A. B.
B.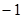 C.
C. D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2010-2011年河北冀州中学高一年级下学期期末考试文科数学(B卷) 题型:选择题
已知平面区域 由以
由以 、
、 、
、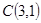 为顶点的三角形内部和边界组成.若在区域
为顶点的三角形内部和边界组成.若在区域 上有无穷多个点
上有无穷多个点 可使目标函数
可使目标函数 取得最小值,则
取得最小值,则 ( )
( )








查看答案和解析>>
科目:高中数学 来源:2010-2011年河北冀州中学高一年级下学期期末考试文科数学(A卷) 题型:选择题
已知平面区域 由以
由以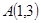 、
、 、
、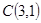 为顶点的三角形内部和边界组成.若在区域
为顶点的三角形内部和边界组成.若在区域 上有无穷多个点
上有无穷多个点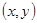 可使目标函数
可使目标函数 取得最小值,则
取得最小值,则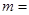 ( )
( )








查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com