
(本题满分12分)
已知a∈R,函数f(x)=4x3-2ax+a.
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+|2-a|>0.
(1)函数f(x)的单调递增区间为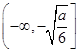 和
和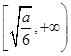 ,
,
单调递减区间为 .(2)见解析。
.(2)见解析。
解析试题分析:(1)根据函数的导数符号与函数单调性的关系来判定求解其单调区间。
(2)要证明不等式恒成立问题,那么要转化为函数的最值问题来处理即可或者构造函数求解函数的 最小值大于零得到。
解:
(1)由题意得f′(x)=12x2-2a.
当a≤0时,f′(x)≥0恒成立,此时f(x)的单调递增区间为(-∞,+∞).
当a>0 时,f′(x)=12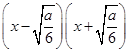 ,此时
,此时
函数f(x)的单调递增区间为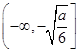 和
和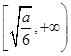 ,
,
单调递减区间为 .
.
(2)由于0≤x≤1,故
当a≤2时,f(x)+|a-2|=4x3-2ax+2≥4x3-4x+2.
当a>2时,f(x)+|a-2|=4x3+2a(1-x)-2≥4x3+4(1-x)-2=4x3-4x+2.
设g(x)=2x3-2x+1,0≤x≤1,则g′(x)=6x2-2=6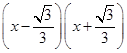 ,于是
,于是
所以g(x)min=g
x
0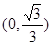
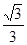
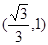
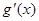
- 0 + 
1 减函数 极小值 增函数 1 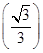 =1-
=1-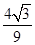 >0.
>0.
所以当0≤x≤1时,2x3-2x+1>0.
故f(x)+|a-2|≥4x3-4x+2>0.
考点:本试题主要考查了导数在研究函数问题中的运用。
点评:对于含有参数的二次不等式问题的求解是解决导数中常见的非常重要的,注意对于开口和判别式的情况进行分类讨论得到结论。


科目:高中数学 来源: 题型:解答题
(本题满分10分) 如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线弧OB上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围成的三角形PQA面积最大。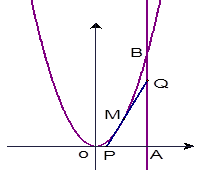
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知函数f(x)=x3+ax2+(a+6)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是3,求a,b的值;
(2)若f(x)为R上的单调递增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
已知函数 (
( ),
), .
.
(Ⅰ)当 时,解关于
时,解关于 的不等式:
的不等式: ;
;
(Ⅱ)当 时,记
时,记 ,过点
,过点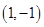 是否存在函数
是否存在函数 图象的切线?若存在,有多少条?若不存在,说明理由;
图象的切线?若存在,有多少条?若不存在,说明理由;
(Ⅲ)若 是使
是使 恒成立的最小值,对任意
恒成立的最小值,对任意 ,
,
试比较 与
与 的大小(常数
的大小(常数 ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
已知函数 .
.
(Ⅰ)求函数 的极大值;
的极大值;
(Ⅱ)若 对满足
对满足 的任意实数
的任意实数 恒成立,求实数
恒成立,求实数 的取值范围(这里
的取值范围(这里 是自然对数的底数);
是自然对数的底数);
(Ⅲ)求证:对任意正数 、
、 、
、 、
、 ,恒有
,恒有
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com