
【题目】已知函数![]() 其图像的一个对称中心是
其图像的一个对称中心是![]() 将
将![]() 的图像向左平移
的图像向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像。
的图像。
(1)求函数![]() 的解析式;
的解析式;
(2)若对任意![]() 当
当![]() 时,都有
时,都有![]() 求实数
求实数![]() 的最大值;
的最大值;
(3)若对任意实数![]() 在
在![]() 上与直线
上与直线![]() 的交点个数不少于6个且不多于10个,求正实数
的交点个数不少于6个且不多于10个,求正实数![]() 的取值范围。
的取值范围。
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC=![]() BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
(1)证明:B1E∥平面ACF;
(2)求平面ADB1与平面ECB1所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|,当a<b<c时,f(a)>f(c)>f(b),那么正确的结论是( )
A.2a>2b
B.2a>2c
C.2﹣a<2c
D.2a+2c<2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知摄影爱好者的身高约为
,已知摄影爱好者的身高约为![]() 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按![]() 米处理).
米处理).
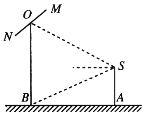
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB;
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角![]() (设为
(设为![]() )是否存在最大值?若存在,请求出
)是否存在最大值?若存在,请求出![]() 取最大值时
取最大值时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)六个从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有几种?
(2)把5件不同产品摆成一排,若产品![]() 与产品
与产品![]() 相邻,且产品
相邻,且产品![]() 与产品
与产品![]() 不相邻,则不同的摆法有几种?
不相邻,则不同的摆法有几种?
(3)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法有几种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-sin2x+mcosx-1,x∈[![]() ].
].
(1)若f(x)的最小值为-4,求m的值;
(2)当m=2时,若对任意x1,x2∈[-![]() ]都有|f(x1)-f(x2)|
]都有|f(x1)-f(x2)|![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产产品![]() 件的总成本
件的总成本![]() (万元).已知产品单价
(万元).已知产品单价![]() (万元)与产品件数
(万元)与产品件数![]() 满足
满足![]() ,生产100件这样的产品单价为50万元.
,生产100件这样的产品单价为50万元.
(1)设产量为![]() 件时,总利润为
件时,总利润为![]() (万元),求
(万元),求![]() 的解析式;
的解析式;
(2)产量![]() 定为多少时总利润
定为多少时总利润![]() (万元)最大?并求最大值.
(万元)最大?并求最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com