
����Ŀ��ij�����̴����ˮ����ֳ������һ��С��Ϻ���������ȡ40ֻ����ͳ�ƣ�����������ͳ�ƽ������ͼ��

��1�����¼�![]() Ϊ����������С��Ϻ����ȡһֻ������������35
Ϊ����������С��Ϻ����ȡһֻ������������35![]() ��С��Ϻ������
��С��Ϻ������![]() �Ĺ���ֵ��
�Ĺ���ֵ��
��2������������С��Ϻ100ǧ�ˣ��Թ�������С��Ϻ��������
��3��Ϊ��Ӧ�г������˽�����С��Ϻ�ĿڸУ��þ����̽���40ֻС��Ϻ�ֳ������ȼ������±���
�ȼ� | һ��Ʒ | ����Ʒ | ����Ʒ |
������ |
|
|
|
���ֲ������ȡ10ֻ���������ȡ3ֻƷ������![]() Ϊ�鵽����Ʒ����������鵽����Ʒ��������
Ϊ�鵽����Ʒ����������鵽����Ʒ��������
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
�������������������1������![]() ֻС��Ϻ������������
ֻС��Ϻ������������![]() ��С��Ϻ��28��������ã�
��С��Ϻ��28��������ã�
��2����ͳ��ͼ�п��Թ���ÿֻС��Ϻ������28.5�ˣ����ɹ���100ǧ��С��Ϻ��������
��3��������֪��ȡһ��Ʒ������Ʒ������Ʒ�ֱ�Ϊ![]() ֻ��
ֻ��![]() ֻ��
ֻ��![]() ֻ��
ֻ�� ![]() �ֱ�����ʣ�����������ʽ������������.
�ֱ�����ʣ�����������ʽ������������.
���������
��1������![]() ֻС��Ϻ������������
ֻС��Ϻ������������![]() ��С��Ϻ��
��С��Ϻ��![]() ��ֻ��
��ֻ��
����![]()
��2����ͳ��ͼ�п��Թ���ÿֻС��Ϻ������
![]()
![]() ���ˣ�
���ˣ�
���Թ���![]() ǧ�ˣ�С��Ϻ������Լ��
ǧ�ˣ�С��Ϻ������Լ��![]() ��ֻ��
��ֻ��
��3��������֪��ȡһ��Ʒ������Ʒ������Ʒ�ֱ�Ϊ![]() ֻ��
ֻ��![]() ֻ��
ֻ��![]() ֻ��
ֻ�� ![]()
��ɵ�![]() ��
�� ![]()
![]() ��
�� ![]()
����![]()


 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�������ܹ���һ�����ϵ��ǣ� ��
A.������20�ķǸ�ʵ��
B.����x2��9=0��ʵ����Χ�ڵĽ�
C.![]() �Ľ���ֵ��ȫ��
�Ľ���ֵ��ȫ��
D.�ٴ�ʮ��2016����У���߳���170����ͬѧ��ȫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ���溯����
���溯����
��1����ʵ��a��ֵ��
��2���жϺ���f��x���ĵ����ԣ�������֤����
��3������f��x����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У��ı���
�У��ı���![]() �����Σ�
�����Σ� ![]() �DZ߳�Ϊ2���������Σ�
�DZ߳�Ϊ2���������Σ� ![]() ��
�� ![]() ��
��
��1��֤���� ![]() ��
��
��2������![]() ��ƽ��
��ƽ��![]() �ڵ���Ӱ
�ڵ���Ӱ![]() ����
����![]() ��ƽ��
��ƽ��![]() ���ɵĽǵ�����ֵ��
���ɵĽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��![]() Ϊ��Ȼ�����ĵ�������
Ϊ��Ȼ�����ĵ�������
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ��
ʱ�� ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ����ֱ��
��Բ����ֱ��![]() ��
�� ![]() �ϣ���ֱ��
�ϣ���ֱ��![]() ��
�� ![]() ���У��ҽ�ֱ��
���У��ҽ�ֱ��![]() ��
�� ![]() �����ҳ�Ϊ6
�����ҳ�Ϊ6
������Բ![]() �ķ���
�ķ���
������![]() �Ƿ����ֱ��
�Ƿ����ֱ��![]() ��ʹ��
��ʹ��![]() ��Բ
��Բ![]() �ص���
�ص���![]() Ϊֱ����Բ����ԭ��?�����ڣ�д��ֱ�ߵķ��̣��������ڣ�˵������.
Ϊֱ����Բ����ԭ��?�����ڣ�д��ֱ�ߵķ��̣��������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
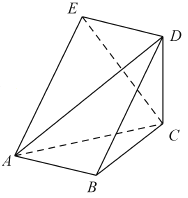
����Ŀ����ͼ![]() ��ֱ������������
��ֱ������������![]() �ǵ���ֱ�������Σ���
�ǵ���ֱ�������Σ���![]() ��ֱ�������ĸߵ���4���߶�
��ֱ�������ĸߵ���4���߶�![]() ���е�Ϊ
���е�Ϊ![]() ���߶�
���߶�![]() ���е�Ϊ
���е�Ϊ![]() ���߶�
���߶�![]() ���е�Ϊ
���е�Ϊ![]() ��
��
��1��������ֱ��![]() ��
��![]() ���ɽǵĴ�С��
���ɽǵĴ�С��
��2��������![]() �������
�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
(I)����![]() �ĶԳ��᷽�̣�
�ĶԳ��᷽�̣�
(II)������![]() ��ͼ���ϸ���������걣�ֲ��䣬�������쳤Ϊԭ����2����Ȼ��������ƽ��
��ͼ���ϸ���������걣�ֲ��䣬�������쳤Ϊԭ����2����Ȼ��������ƽ��![]() ����λ���õ�����
����λ���õ�����![]() ��ͼ����
��ͼ����![]() �ֱ��ǡ�ABC�����ڽ�A��B��C�ĶԱߣ�a=2��c=4����
�ֱ��ǡ�ABC�����ڽ�A��B��C�ĶԱߣ�a=2��c=4����![]() ����b��ֵ��
����b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() :
:![]()
![]() �ϵ���һ�㵽����ľ������ֵΪ3��������Ϊ
�ϵ���һ�㵽����ľ������ֵΪ3��������Ϊ![]() ��
��
��1������Բ![]() �ı����̣�
�ı����̣�
��2����![]() ����
Ϊ����![]() �����㣬
�����㣬 ![]() Ϊ����ԭ�㣬ֱ��
Ϊ����ԭ�㣬ֱ��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ����
����![]() ����ֱ��
����ֱ��![]() ��Բ
��Բ![]() �ص��ҳ������ֵ����ʱֱ��
�ص��ҳ������ֵ����ʱֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com