
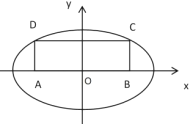
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() ,
,![]() 为焦点的椭圆
为焦点的椭圆![]() :
:![]() 恰好过
恰好过![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,直线
为原点,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 在
在![]() 轴异侧,若
轴异侧,若![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】(2015秋运城期中)已知函数f(x)=(log2x﹣2)(log4x﹣![]() ).
).
(1)当x∈[1,4]时,求该函数的值域;
(2)若f(x)≤mlog2x对于x∈[4,16]恒成立,求m得取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级共有1000 名学生,为了了解学生返校上课前口罩准备的情况,学校统计了所有学生口罩准备的数量,并绘制了如下频率分布直方图.

(1)求![]() 的值;
的值;
(2)现用分层抽样的方法,从口罩准备数量在![]() 和
和![]() 的学生中选10人参加视频会议,则两组各选多少人?
的学生中选10人参加视频会议,则两组各选多少人?
(3)在(2)的条件下,从参加视频会议的10人中随机抽取3人,参与学校组织的复学演练.记![]() 为这3人中口罩准备数量在
为这3人中口罩准备数量在![]() 的学生人数,求
的学生人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2ωx+![]() )+sin(2ωx-
)+sin(2ωx-![]() )+2cos2ωx,其中ω>0,且函数f(x)的最小正周期为π
)+2cos2ωx,其中ω>0,且函数f(x)的最小正周期为π
(1)求ω的值;
(2)求f(x)的单调增区间
(3)若函数g(x)=f(x)-a在区间[-![]() ,
,![]() ]上有两个零点,求实数a的取值范围.
]上有两个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】服装销售商甲和乙欲销某品牌服装制造企业生产的服装. 该企业的设计部门在无任何有关甲和乙销售信息的情况下,随机地为他们提供了![]() 种不同设计的款式,由甲和乙各自独立地选定自己认可的那些款式. 则至少有一个款式为甲和乙共同认可的概率为多少?
种不同设计的款式,由甲和乙各自独立地选定自己认可的那些款式. 则至少有一个款式为甲和乙共同认可的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com