
【题目】已知函数![]() ,令
,令![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值;
的最小值;
(3)若![]() ,正实数
,正实数![]() 满足
满足![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() (2)最小值为
(2)最小值为![]() .(3)见解析
.(3)见解析
【解析】试题分析:(1)求出导函数并由导函数大于零求出不等式的解,从而得到函数的单调递增区间;(2)又不等式求参数范围,常常把不等式化为一边是零的形式即![]() 等价于
等价于![]() ,接下来对参数m讨论求函数
,接下来对参数m讨论求函数![]() 的最大值,从而求出m的最小值.(3)构造创设出关于
的最大值,从而求出m的最小值.(3)构造创设出关于![]() 的不等式,从而得证.
的不等式,从而得证.
试题解析:(1)![]()
![]()
由![]() 得
得![]() 又
又![]() 所以
所以![]() .所以
.所以![]() 的单增区间为
的单增区间为![]() .
.
(2)令![]()
所以![]() .
.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 所以
所以![]() 在
在![]() 上是递增函数,
上是递增函数,
又因为![]()
所以关于![]() 的不等式
的不等式![]() 不能恒成立.
不能恒成立.
当![]() 时,
时, 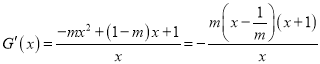 .
.
令![]() 得
得![]() ,所以当
,所以当![]() 时,
时, ![]() 当
当![]() 时,
时, ![]() .
.
因此函数![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数.
是减函数.
故函数![]() 的最大值为
的最大值为![]()
令![]() 因为
因为![]()
又因为![]() 在
在![]() 上是减函数,所以当
上是减函数,所以当![]() 时,
时, ![]() .
.
所以整数![]() 的最小值为2.
的最小值为2.
(3)当![]() 时,
时, ![]()
由![]() 即
即![]()
从而![]()
令![]() 则由
则由![]() 得,
得, ![]()
可知![]() 在区间(0,1)上单调递减,在区间
在区间(0,1)上单调递减,在区间![]() 上单调递增.所以
上单调递增.所以![]()
所以![]() 即
即![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】将正方形![]() 沿对角线
沿对角线![]() 折成直二面角
折成直二面角![]() ,有如下四个结论:
,有如下四个结论:
①![]() ;
;
②![]() 是等边三角形;
是等边三角形;
③![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;
;
④![]() 与
与![]() 所成的角为
所成的角为![]() .
.
其中错误的结论是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:

(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm的概率;
(3)从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为集合
为集合![]() 的子集,且
的子集,且![]() ,若
,若![]() ,则称
,则称![]() 为集合
为集合![]() 的
的![]() 元“大同集”.
元“大同集”.
(1)写出实数集![]() 的一个二元“大同集”;
的一个二元“大同集”;
(2)是否存在正整数集![]() 的二元“大同集”,请说明理由;
的二元“大同集”,请说明理由;
(3)求出正整数集![]() 的所有三元“大同集”.
的所有三元“大同集”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,定义域为![]() 上的函数
上的函数![]() 是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.
是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.

(1)求![]() 的解析式;
的解析式;
(2)若![]() 关于的方程
关于的方程![]() 有三个不同解,求
有三个不同解,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的取值集合.
的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com