
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 引圆
引圆![]() 的两条切线
的两条切线![]() ,切线
,切线![]() 与抛物线
与抛物线![]() 的另一交点分别为
的另一交点分别为![]() ,线段
,线段![]() 中点的横坐标记为
中点的横坐标记为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某超市2019年中的12个月的收入与支出数据的折线图如图所示,则下列说法中,错误的是( )
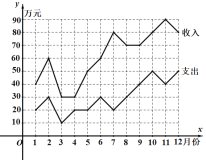
A.该超市在2019年的12个月中,7月份的收益最高;
B.该超市在2019年的12个月中,4月份的收益最低;
C.该超市在2019年7月至12月的总收益比2109年1月至6月的总收益增长了90万元;
D.该超市在2019年1月至6月的总收益低于2109年7月至12月的总收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,E是棱
的中点,E是棱![]() 上一动点.
上一动点.
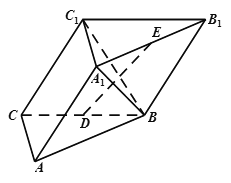
(1)若E是棱![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)是否存在点E,使得![]() ,若存在,求出E的坐标,若不存在,说明理由.
,若存在,求出E的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,抛物线
,抛物线![]() 的焦点
的焦点![]() 恰好是该椭圆的一个顶点.
恰好是该椭圆的一个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 相切,且直线
相切,且直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县为了帮助农户脱贫致富,鼓励农户利用荒地山坡种植果树,某农户考察了三种不同的果树苗![]() 、
、![]() 、
、![]() .经过引种实验发现,引种树苗
.经过引种实验发现,引种树苗![]() 的自然成活率为
的自然成活率为![]() ,引种树苗
,引种树苗![]() 、
、![]() 的自然成活率均为
的自然成活率均为![]() .
.
(1)任取树苗![]() 、
、![]() 、
、![]() 各一棵,估计自然成活的棵数为
各一棵,估计自然成活的棵数为![]() ,求
,求![]() 的分布列及其数学期望;
的分布列及其数学期望;
(2)将(1)中的数学期望取得最大值时![]() 的值作为
的值作为![]() 种树苗自然成活的概率.该农户决定引种
种树苗自然成活的概率.该农户决定引种![]() 棵
棵![]() 种树苗,引种后没有自然成活的树苗有
种树苗,引种后没有自然成活的树苗有![]() 的树苗可经过人工栽培技术处理,处理后成活的概率为
的树苗可经过人工栽培技术处理,处理后成活的概率为![]() ,其余的树苗不能成活.
,其余的树苗不能成活.
①求一棵![]() 种树苗最终成活的概率;
种树苗最终成活的概率;
②若每棵树苗引种最终成活可获利![]() 元,不成活的每棵亏损
元,不成活的每棵亏损![]() 元,该农户为了获利期望不低于
元,该农户为了获利期望不低于![]() 万元,问至少要引种
万元,问至少要引种![]() 种树苗多少棵?
种树苗多少棵?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,点
,点![]() ,点
,点![]() 、
、![]() 分别为椭圆的上顶点和左焦点,且
分别为椭圆的上顶点和左焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过定点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() ,
,![]() 之间)设直线
之间)设直线![]() 的斜率
的斜率![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() ,
,![]() 为邻边的平行四边形为菱形?如果存在,求出
为邻边的平行四边形为菱形?如果存在,求出![]() 的取值范围?如果不存在,请说明理由.
的取值范围?如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,极坐标系中
,极坐标系中![]() ,弧
,弧![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
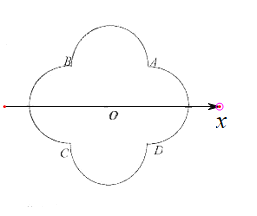
(1)分别写出![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 有两个不同交点
有两个不同交点![]() ,求实数
,求实数![]() 的取值范围,并求出
的取值范围,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com