
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(3)已知![]() ,且任意
,且任意![]() 有
有![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)![]() ;(2)分类讨论,详见解析;(3)
;(2)分类讨论,详见解析;(3)![]() .
.
【解析】
(1)当x>1时,f(x)=x3+3x﹣3,f(2)=11.由f'(x)=3x2+3,得f'(2)=15.由此利用导数的几何意义能求出y=f(x)在x=2处的切线方程;
(2)当a≤﹣1时,得f(x)=x3+3x﹣3a,由f'(x)=3x2+3>0,得到f(x)min=f(﹣1)=﹣4﹣3a.当a≥1时,得f(x)=x3﹣3x+3a,由f'(x)=3x2﹣3≤0,得到f(x)min=f(1)=﹣2+3a.当﹣1<a<1时,f(x) ,由此能求出函数f(x)的最小值;
,由此能求出函数f(x)的最小值;
(3)当a>0,且任意x≥1有f(x+a)﹣f(1+a)≥15a2lnx,即对任意x≥1有(x+a)3+3x﹣15a2lnx﹣(a+1)3﹣3≥0.设g(x)=(x+a)3+3x﹣15a2lnx﹣(a+1)3﹣3,则g(1)=0,g'(x)=3(x+a)2+3![]() .设h(x)=g'(x)=3(x+a)2+3
.设h(x)=g'(x)=3(x+a)2+3![]() ,则h'(x)=6(x+a)
,则h'(x)=6(x+a)![]() 0,由此利用导数性质能求出结果.
0,由此利用导数性质能求出结果.
解:(1)当![]() 时,
时,![]() ,
,![]() .由
.由![]() ,得
,得![]() .
.
所以![]() 在
在![]() 处的切线方程为
处的切线方程为![]() 即
即![]() .
.
(2)①当![]() 时,得
时,得![]() ,因为
,因为![]() ,
,
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() .
.
②当![]() 时,得
时,得![]() ,因为
,因为![]() ,
,
所以![]() 在
在![]() 单调递减,所以
单调递减,所以![]() .
.
③当![]() 时,
时,
由①②知:函数![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,所以
单调递增,所以![]() ,
,
综上,当![]() ,
,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
(3)当![]() ,且任意
,且任意![]() 有
有![]() ,
,
即对任意![]() 有
有![]() .
.
设![]() ,
,
则![]() ,
,![]() .
.
设![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() ,
,
①当![]() 即
即![]() 时,所以
时,所以![]() 恒成立,
恒成立,
所以![]() 在
在![]() 单调递增,此时
单调递增,此时![]() ,满足题意.
,满足题意.
②当![]() 即
即![]() 时,
时,
因为![]() ,且
,且![]() 在
在![]() 单调递增,
单调递增,
所以存在唯一的![]() ,使得
,使得![]() ,
,
因此当![]() 时
时![]() ;当
;当![]() 时
时![]() ;
;
所以![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增.
单调递增.
所以![]() ,不满足题意.
,不满足题意.
综上,![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2![]() ,BC=6.
,BC=6.
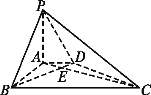
(1)求证:BD⊥平面PAC; (2)求二面角P-BD-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
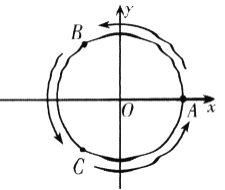
【题目】如图,直角坐标系中,圆的方程为![]() ,
,![]() ,
,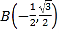 ,
,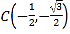 为圆上三个定点,某同学从
为圆上三个定点,某同学从![]() 点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子
点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子![]() 次时,棋子移动到
次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .例如:掷骰子一次时,棋子移动到
.例如:掷骰子一次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .
.
(1)分别掷骰子二次,三次时,求棋子分别移动到![]() ,
,![]() ,
,![]() 处的概率;
处的概率;
(2)掷骰子![]() 次时,若以
次时,若以![]() 轴非负半轴为始边,以射线
轴非负半轴为始边,以射线![]() ,
,![]() ,
,![]() 为终边的角的余弦值记为随机变量
为终边的角的余弦值记为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记![]() ,
,![]() ,
,![]() ,其中
,其中![]() .证明:数列
.证明:数列![]() 是等比数列,并求
是等比数列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线C:x2=4y的准线上任意一点P作抛物线的切线PA,PB,切点分别为A,B,则A点到准线的距离与B点到准线的距离之和的最小值是( )
A.7B.6C.5D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是五四运动100周年.五四运动以来的100年,是中国青年一代又一代接续奋斗、凯歌前行的100年,是中口青年用青春之我创造青春之中国、青春之民族的100年.为继承和发扬五四精神在青年节到来之际,学校组织“五四运动100周年”知识竞赛,竞赛的一个环节由10道题目组成,其中6道A类题、4道B类题,参赛者需从10道题目中随机抽取3道作答,现有甲同学参加该环节的比赛.
(1)求甲同学至少抽到2道B类题的概率;
(2)若甲同学答对每道A类题的概率都是![]() ,答对每道B类题的概率都是
,答对每道B类题的概率都是![]() ,且各题答对与否相互独立.现已知甲同学恰好抽中2道A类题和1道B类题,用X表示甲同学答对题目的个数,求随机变量X的分布列和数学期望.
,且各题答对与否相互独立.现已知甲同学恰好抽中2道A类题和1道B类题,用X表示甲同学答对题目的个数,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com