
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 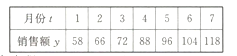
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
, ![]() .
.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某校10位同学组成的志愿者组织分别由李老师和杨老师负责.每次献爱心活动均需该组织4位同学参加.假设李老师和杨老师分别将各自活动通知的信息独立、随机地发给4位同学,且所发信息都能收到.则甲同学收到李老师或杨老师所发活动通知信息的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一张坐标纸上涂着圆E: ![]() 及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
(1)求 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(2)直线 ![]() 与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若
与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若 ![]() ,求△ABO的面积的取值范围.
,求△ABO的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题: ①已知随机变量X~N(0,σ2),若P(|X|<2)=a,则P(X>2)的值为 ![]() ;
;
②设a、b∈R,则“log2a>log2b”是“2a﹣b>1”的充分不必要条件;
③函数f(x)= ![]() ﹣(
﹣( ![]() )x的零点个数为1;
)x的零点个数为1;
④命题p:n∈N,3n≥n2+1,则¬p为n∈N,3n≤n2+1.
其中真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的两个焦点为F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0),M是椭圆上一点,若
,0),M是椭圆上一点,若 ![]()
![]() =0,|
=0,| ![]() ||
|| ![]() |=8.
|=8.
(1)求椭圆的方程;
(2)点P是椭圆上任意一点,A1、A2分别是椭圆的左、右顶点,直线PA1 , PA2与直线x= ![]() 分别交于E,F两点,试证:以EF为直径的圆交x轴于定点,并求该定点的坐标.
分别交于E,F两点,试证:以EF为直径的圆交x轴于定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, ![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 时从区间
时从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形SABC中,∠B=∠C= ![]() ,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB. 
(1)求证:PD⊥平面ABCD;
(2)已知PD=AD,PD+AD+DC=6,G是AD的中点,当线段PB取得最小值时,则在平面PBC上是否存在点F,使得FG⊥平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ,以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于
,以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于 ![]() 四点,四边形
四点,四边形 ![]() 的面积为
的面积为 ![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.![]()
B.2
C.![]()
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com